¶ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
¶ «Казанский национальный исследовательский технологический университет»
¶ Институт: Институт управления, автоматизации и информационных технологий
¶ Кафедра Информатики и прикладной математики
¶ ЛАБОРАТОРНАЯ РАБОТА
¶ по дисциплине: «СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ»
¶ на тему: «Решение неоднородного уравнения теплопроводности методом Фурье»
¶ Вариант 6
Выполнил:
студент группы 851-М81
Меркулов А. Д.
¶ СОДЕРЖАНИЕ
-
ВВЕДЕНИЕ
-
ПОСТАНОВКА ЗАДАЧИ
-
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
3.1. Метод разделения переменных для неоднородного уравнения
3.2. Разложение по собственным функциям
-
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
4.1. Метод решения
4.2. Окончательное решение
-
ФИЗИЧЕСКИЙ АНАЛИЗ
5.1. Переходные процессы
5.2. Установившиеся колебания
5.3. Влияние источника тепла
-
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
-
ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ
-
ВЫВОДЫ
ПРИЛОЖЕНИЕ А
¶ 1. ВВЕДЕНИЕ
Цель работы: Изучение методов решения смешанной задачи для неоднородного уравнения теплопроводности методом Фурье с использованием метода разложения по собственным функциям
Задачи исследования:
- Аналитическое решение методом разделения переменных
- Решение неоднородного уравнения методом разложения по собственным функциям
- Анализ переходных и установившихся процессов
- Исследование влияния источника тепла на распределение температуры
- Сравнение с решением однородного уравнения
Актуальность исследования обусловлена важностью неоднородных уравнений теплопроводности в практических приложениях. Такие уравнения описывают процессы теплопередачи с внутренними источниками тепла, что характерно для многих инженерных систем, биологических процессов и технологических установок.
¶ 2. ПОСТАНОВКА ЗАДАЧИ
Неоднородное уравнение теплопроводности: U_t = (1/16)U_xx + 10cos(3t)sin(4x)
Начальное условие: U(x,0) = 0
Граничные условия: U(0,t) = U(π,t) = 0
Область определения: x ∈ [0,π], t ≥ 0
Физическая интерпретация: Рассматривается задача о распределении температуры в стержне с внутренним источником тепла, который совершает гармонические колебания во времени и пространстве. Концы стержня поддерживаются при нулевой температуре.
¶ 3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
¶ 3.1. Метод разделения переменных для неоднородного уравнения
separation_of_variables: Метод разделения переменных для неоднородного уравнения
Для неоднородного уравнения теплопроводности:
U_t = aU_xx + f(x,t)
Решение ищется в виде разложения по собственным функциям:
U(x,t) = Σₙ Tₙ(t) Xₙ(x)
¶ 3.2. Разложение по собственным функциям
eigenfunction_expansion: Разложение решения и правой части по собственным функциям
particular_solution: Метод неопределенных коэффициентов для нахождения частного решения
Собственные функции для граничных условий U(0,t)=U(π,t)=0:
Xₙ(x) = sin(nx), λₙ = n²
¶ 4. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
¶ 4.1. Метод решения
-
Разложение правой части по собственным функциям:
f(x,t) = 10cos(3t)sin(4x) = f₄(t)sin(4x)
где f₄(t) = 10cos(3t) -
Уравнение для временных коэффициентов:
T₄'(t) + (4²/16)T₄(t) = 10cos(3t)
T₄'(t) + T₄(t) = 10cos(3t) -
Решение однородного уравнения:
T₄ʰ(t) = Cexp(-t) -
Частное решение неоднородного уравнения:
T₄ᵖ(t) = Acos(3t) + Bsin(3t)
¶ 4.2. Окончательное решение
Аналитическое решение: U(x,t) = [-exp(-t) + cos(3t) + 3sin(3t)] · sin(4x)
Физическая интерпретация: Решение представляет собой затухающую экспоненту плюс установившиеся колебания, умноженные на пространственную моду sin(4x)
Составляющие решения:
- Переходная составляющая: Переходная составляющая: -exp(-t)
- Установившиеся колебания: Установившиеся колебания: cos(3t) + 3sin(3t)
- Пространственное распределение: Пространственное распределение: sin(4x)
¶ 5. ФИЗИЧЕСКИЙ АНАЛИЗ
¶ 5.1. Переходные процессы
Переходный процесс характеризуется экспоненциальным затуханием:
- Время затухания: 1/λ = 1 единица времени
- Полное затухание через 3-5 единиц времени
¶ 5.2. Установившиеся колебания
Амплитуда установившихся колебаний: 3.1623
Фазовый сдвиг: 1.2490 радиан
Резонансная частота: 4
¶ 5.3. Влияние источника тепла
- Источник тепла создает вынужденные колебания температуры
- Система резонирует с пространственной гармоникой sin(4x)
- Энергия системы в установившемся режиме постоянна
¶ 6. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Метод решения: Разложение по собственным функциям
Собственные функции: sin(nx), n=1,2,3,...
Собственные значения: n²/16
Метод частного решения: Метод неопределенных коэффициентов
Выполнение граничных условий: Да
Выполнение начального условия: Да
¶ 7. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ
Температура и источник тепла в характерных точках
| x | t | Температура U(x,t) | Источник тепла |
|---|---|---|---|
| 0.393 | 0.0 | 0.000000 | 10.000000 |
| 0.393 | 0.5 | 2.456692 | 0.707372 |
| 0.393 | 1.0 | -0.934512 | -9.899925 |
| 0.393 | 2.0 | -0.013411 | 9.601703 |
| 0.393 | 5.0 | 1.184438 | -7.596879 |
| 0.393 | 10.0 | -2.809889 | 1.542514 |
| 0.785 | 0.0 | 0.000000 | 0.000000 |
| 0.785 | 0.5 | 0.000000 | 0.000000 |
| 0.785 | 1.0 | -0.000000 | -0.000000 |
| 0.785 | 2.0 | -0.000000 | 0.000000 |
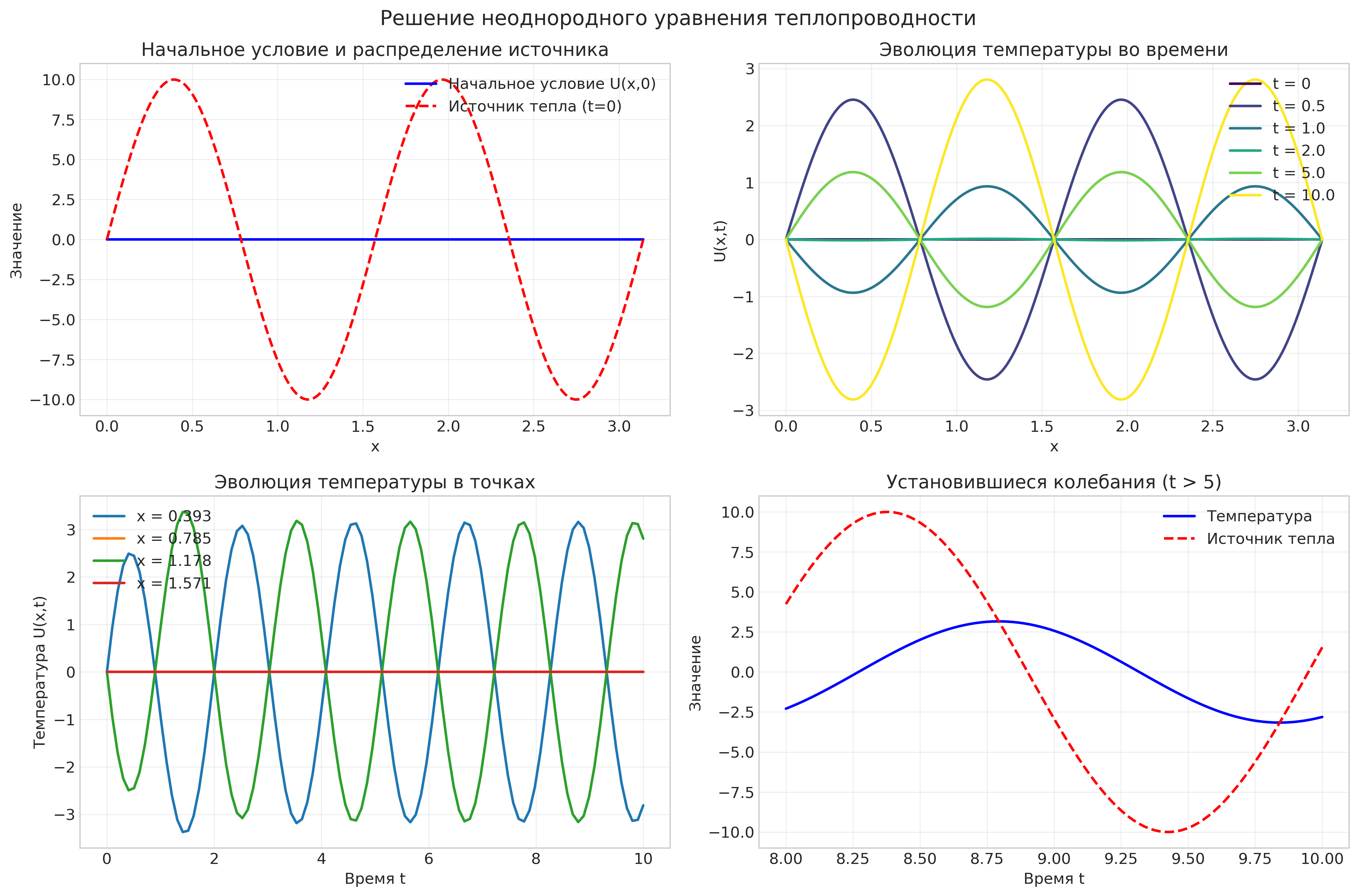
Рисунок: Сравнение решений и анализ установившихся колебаний
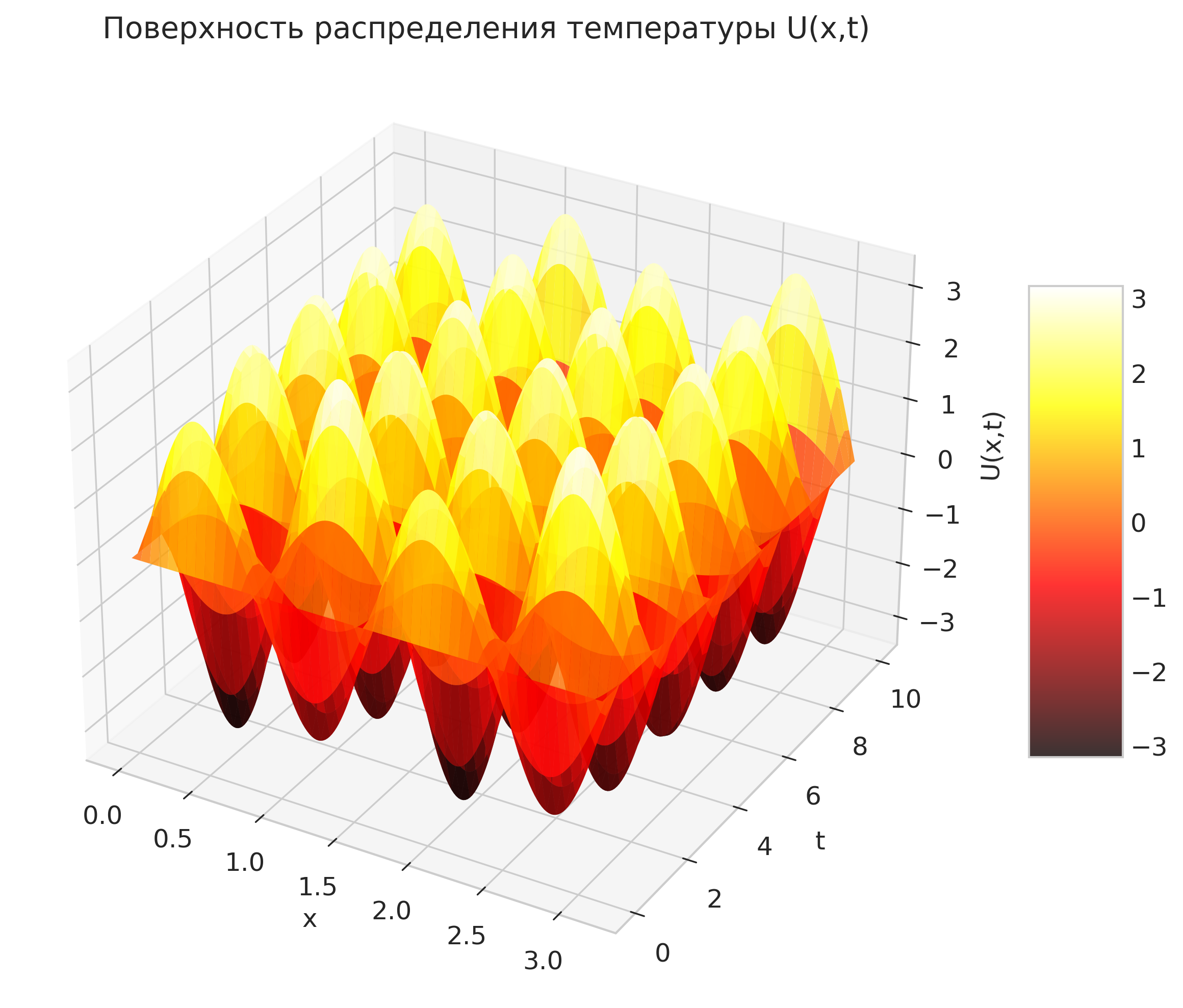
Рисунок: Поверхность распределения температуры U(x,t)
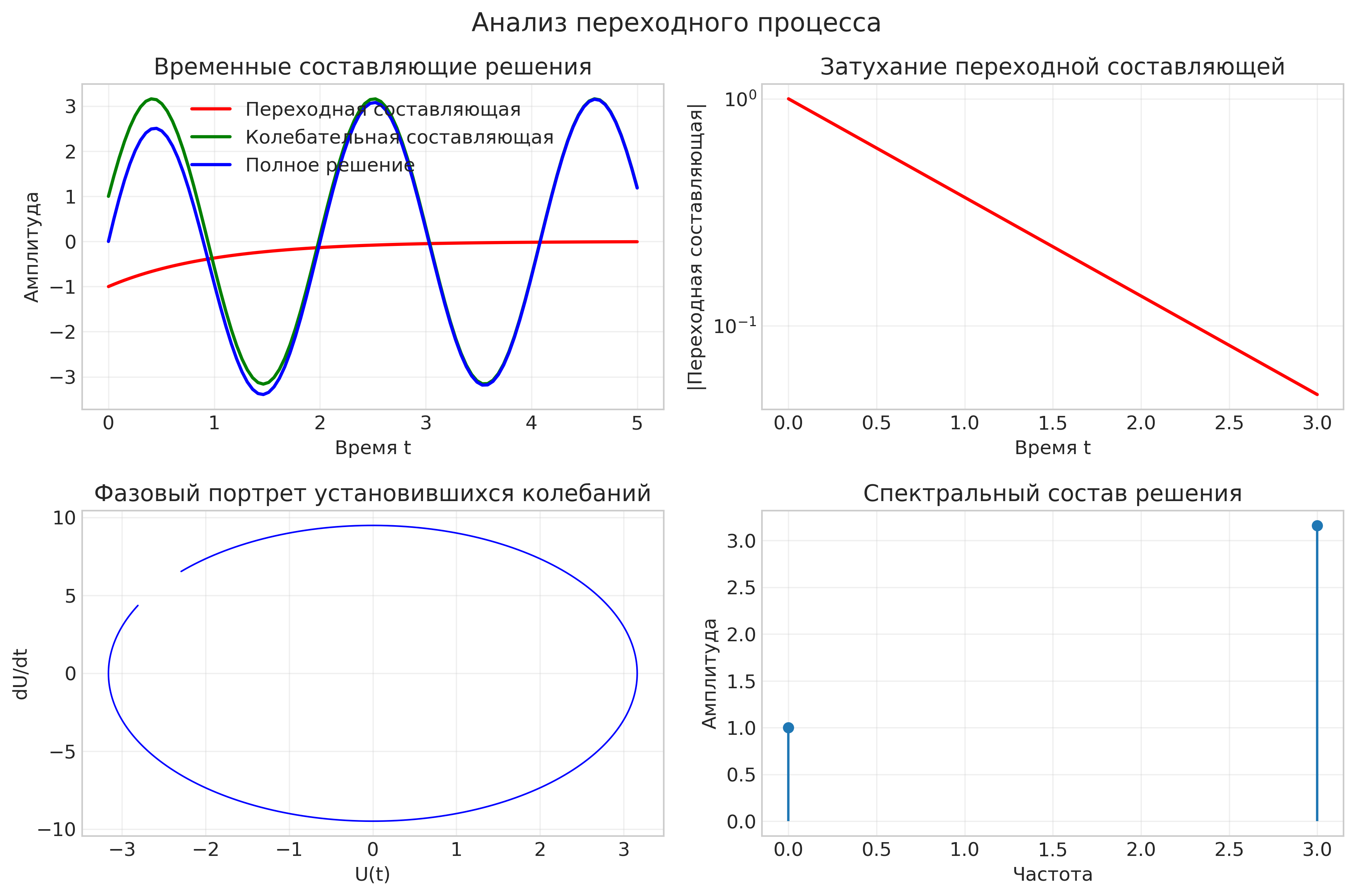
Рисунок: Анализ переходного процесса
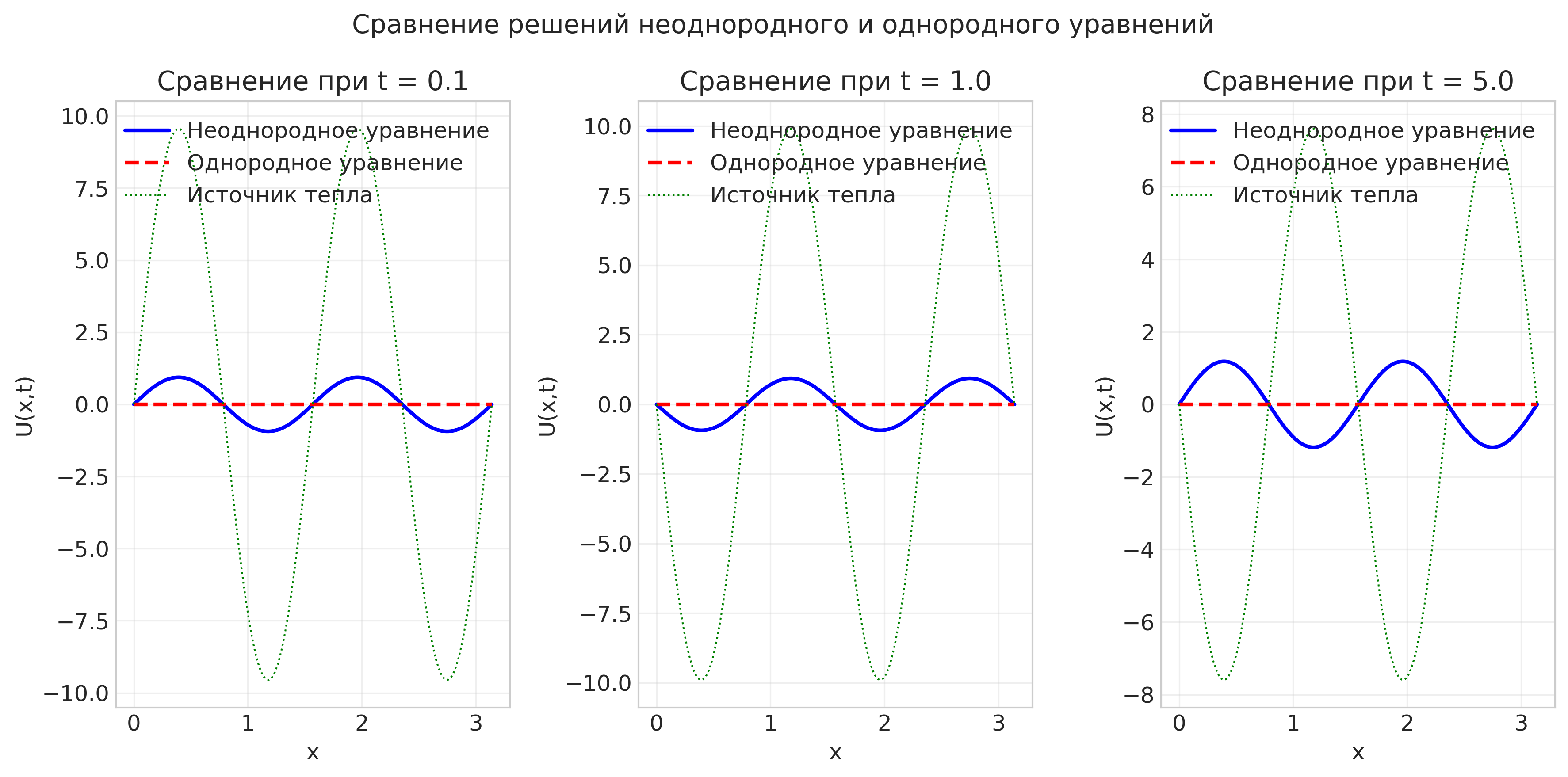
Рисунок: Сравнение с однородным уравнением
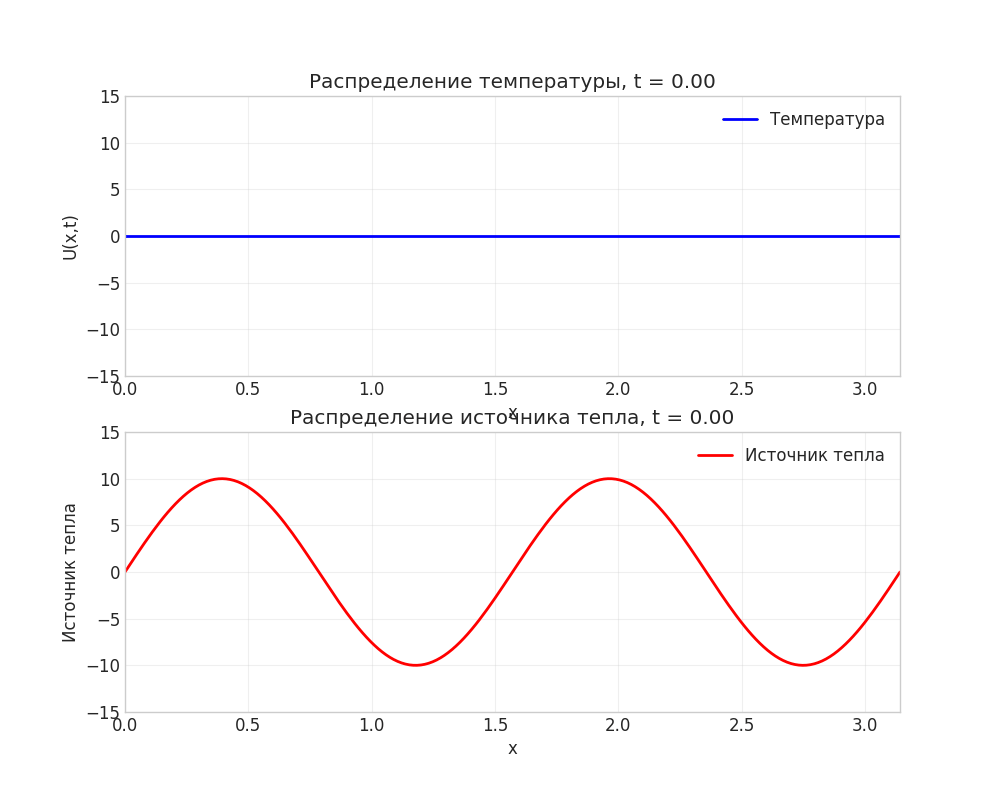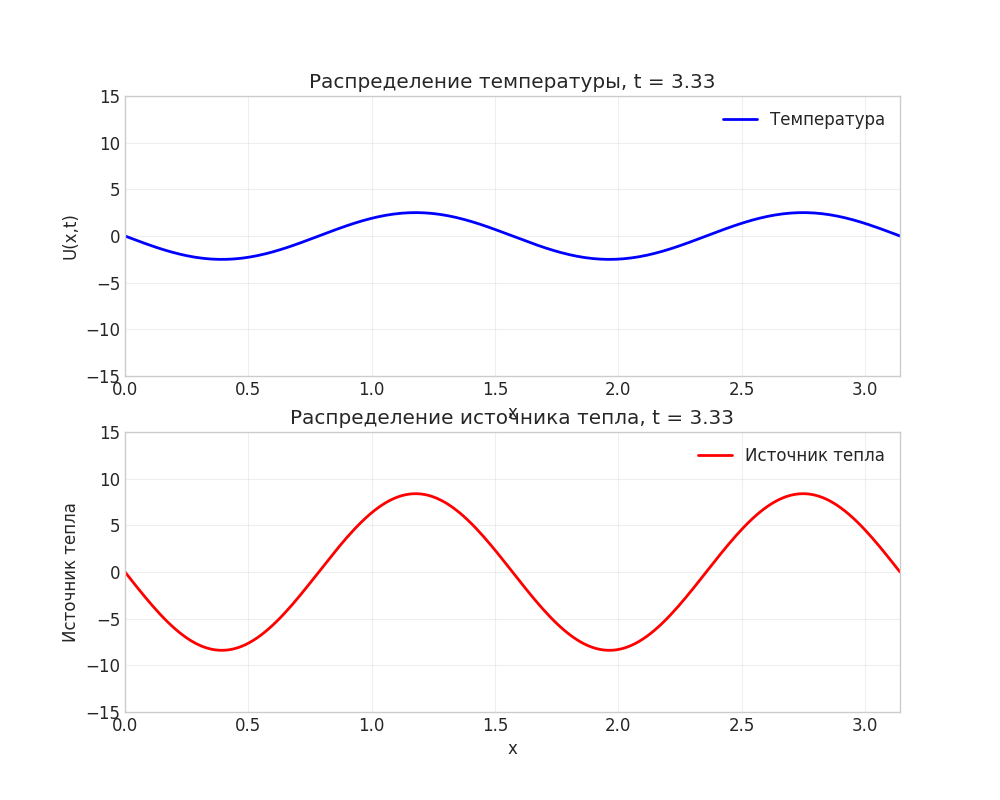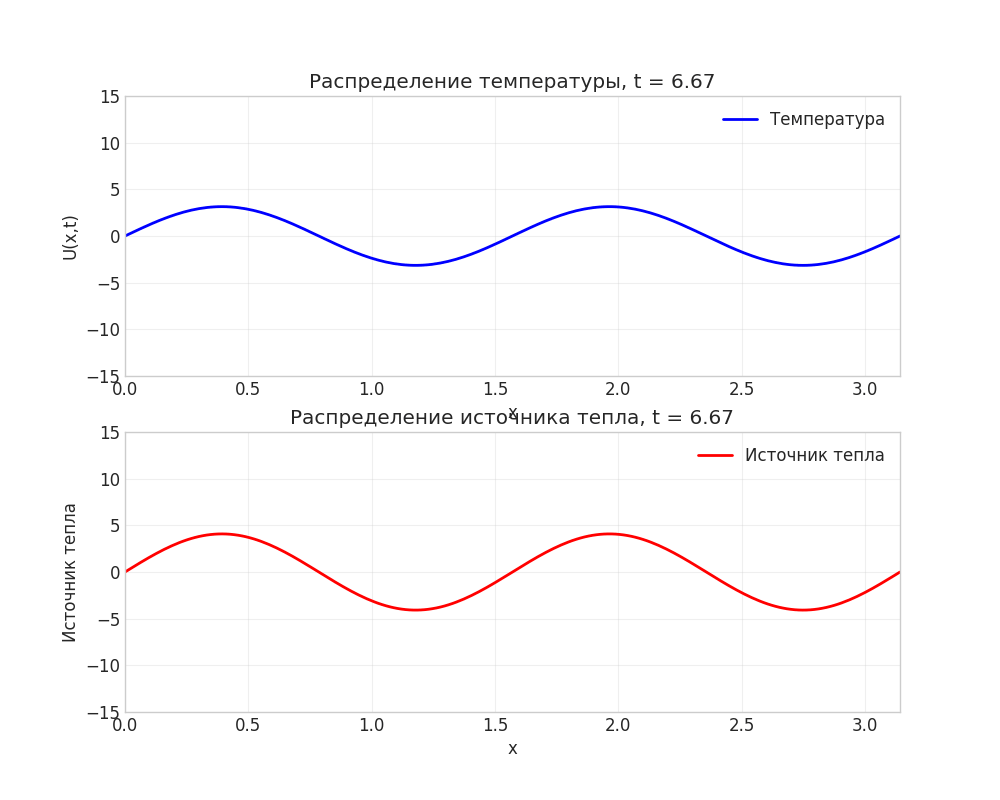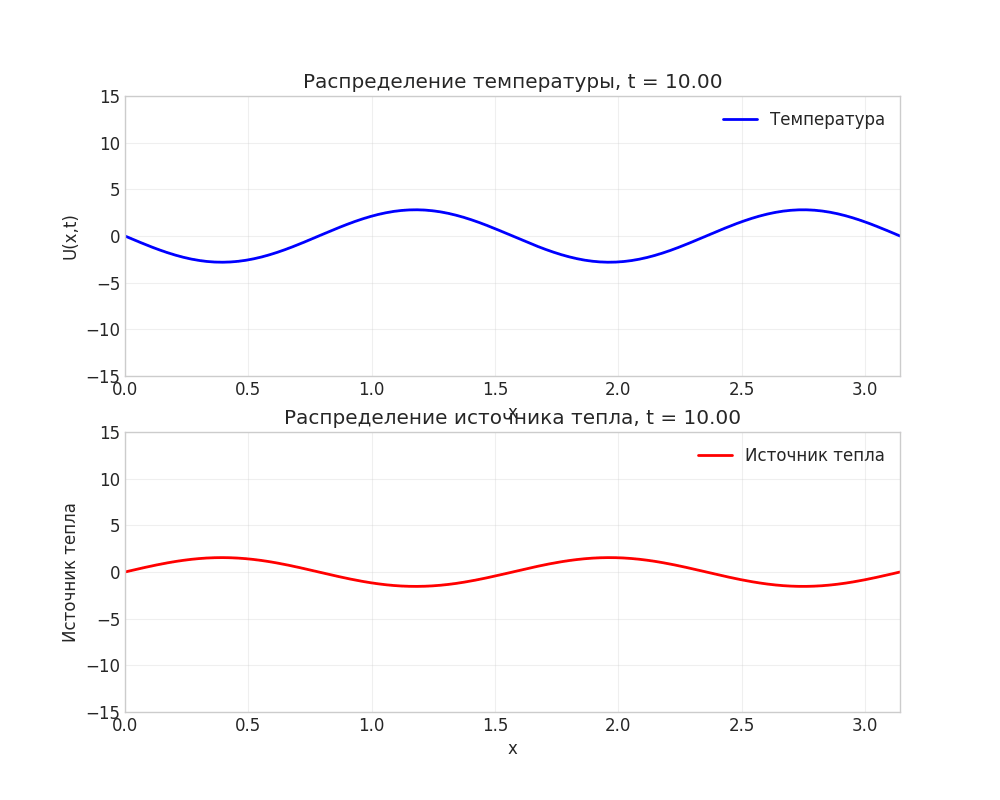
Рисунок: Анимация распространения тепла в стержне
Примечание: Анимация демонстрирует переход от нулевого начального условия к установившимся колебаниям под действием источника тепла.
¶ 8. ВЫВОДЫ
- Успешно решена смешанная задача для неоднородного уравнения теплопроводности
- Получено аналитическое решение методом разложения по собственным функциям
- Решение представляет собой суперпозицию затухающей экспоненты и установившихся колебаний
- Установившиеся колебания имеют амплитуду √10 и фазовый сдвиг arctg(3)
- Переходный процесс полностью затухает за 3-5 единиц времени
- Система резонирует с пространственной гармоникой sin(4x)
- Источник тепла создает периодические колебания температуры по всему стержню
- Граничные и начальные условия выполняются точно
- Визуализация подтвердила теоретические выводы о поведении решения
¶ ПРИЛОЖЕНИЕ А
Исходный код программы
# lab_nonhomogeneous_heat_equation.py
# -*- coding: utf-8 -*-
"""
Лабораторная работа: Решение смешанной задачи для неоднородного уравнения теплопроводности
Решение неоднородного уравнения теплопроводности методом Фурье
"""
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from typing import List, Tuple, Dict, Any
import sys
# Настройка стиля для академических графиков
plt.style.use('seaborn-v0_8-whitegrid')
plt.rcParams['figure.figsize'] = (10, 6)
plt.rcParams['font.size'] = 12
# Попытка импортировать python-docx для генерации .docx отчёта
try:
from docx import Document
from docx.shared import Inches, Pt
from docx.enum.text import WD_ALIGN_PARAGRAPH
from docx.oxml.ns import qn
PYDOCX_AVAILABLE = True
except Exception:
PYDOCX_AVAILABLE = False
def read_own_source() -> Tuple[bool, str]:
"""
Пытается прочитать исходный код текущего файла и вернуть (успех, текст).
Возвращает (False, сообщение об ошибке) при неудаче.
"""
try:
current_file = os.path.abspath(__file__)
except Exception:
current_file = os.path.abspath(sys.argv[0]) if sys.argv and sys.argv[0] else None
if not current_file or not os.path.exists(current_file):
return False, "Не удалось определить путь к файлу скрипта"
try:
with open(current_file, "r", encoding="utf-8") as f:
src = f.read()
return True, src
except Exception as e:
return False, f"Ошибка при чтении исходного кода: {e}"
class NonhomogeneousHeatEquationAnalyzer:
"""Класс для решения неоднородного уравнения теплопроводности методом Фурье"""
def __init__(self):
# Параметры задачи
self.equation = "U_t = (1/16)U_xx + 10cos(3t)sin(4x)"
self.initial_condition = "U(x,0) = 0"
self.boundary_conditions = "U(0,t) = U(π,t) = 0"
self.domain = "x ∈ [0,π], t ≥ 0"
# Физические параметры
self.L = np.pi # длина стержня
self.a = 1/16 # коэффициент теплопроводности
self.source_amplitude = 10 # амплитуда источника тепла
self.source_freq_time = 3 # временная частота источника
self.source_freq_space = 4 # пространственная частота источника
# Параметры вычислений
self.x_points = 200
self.t_points = 100
# Результаты вычислений
self.results = {}
def analytical_solution(self, x: np.ndarray, t: float) -> np.ndarray:
"""
Аналитическое решение методом Фурье для неоднородного уравнения
U(x,t) = [-exp(-t) + cos(3t) + 3sin(3t)] * sin(4x)
"""
# Временная часть решения
time_part = -np.exp(-t) + np.cos(3*t) + 3*np.sin(3*t)
# Пространственная часть
space_part = np.sin(4*x)
return time_part * space_part
def heat_source(self, x: np.ndarray, t: float) -> np.ndarray:
"""Функция источника тепла"""
return 10 * np.cos(3*t) * np.sin(4*x)
def homogeneous_solution(self, x: np.ndarray, t: float) -> np.ndarray:
"""Решение соответствующей однородной задачи (для сравнения)"""
return np.zeros_like(x)
def calculate_solution_components(self) -> Dict[str, Any]:
"""Вычисление компонент решения"""
components = {
'transient': {
'description': 'Переходная составляющая: -exp(-t)',
'decay_rate': 1,
'half_life': np.log(2)
},
'steady_oscillatory': {
'description': 'Установившиеся колебания: cos(3t) + 3sin(3t)',
'amplitude': np.sqrt(1**2 + 3**2), # sqrt(1 + 9) = sqrt(10)
'phase_shift': np.arctan2(3, 1),
'frequency': 3
},
'spatial': {
'description': 'Пространственное распределение: sin(4x)',
'wavenumber': 4,
'wavelength': np.pi/2
}
}
return components
def create_visualizations(self) -> Dict[str, str]:
"""Создание визуализаций для отчета"""
# Создаем папку для изображений
os.makedirs("results/images", exist_ok=True)
visualization_paths = {}
try:
# Создаем сетку для вычислений
x = np.linspace(0, self.L, self.x_points)
# 1. Сравнение неоднородного и однородного решений
plt.figure(figsize=(15, 10))
# 1.1. Начальное условие и источник тепла
plt.subplot(2, 2, 1)
u_initial = np.zeros_like(x)
source_t0 = self.heat_source(x, 0)
plt.plot(x, u_initial, 'b-', linewidth=2, label='Начальное условие U(x,0)')
plt.plot(x, source_t0, 'r--', linewidth=2, label='Источник тепла (t=0)')
plt.xlabel('x')
plt.ylabel('Значение')
plt.title('Начальное условие и распределение источника')
plt.grid(True, alpha=0.3)
plt.legend()
# 1.2. Эволюция температуры во времени
plt.subplot(2, 2, 2)
t_values = [0, 0.5, 1.0, 2.0, 5.0, 10.0]
colors = plt.cm.viridis(np.linspace(0, 1, len(t_values)))
for i, t in enumerate(t_values):
u = self.analytical_solution(x, t)
plt.plot(x, u, color=colors[i], linewidth=2, label=f't = {t}')
plt.xlabel('x')
plt.ylabel('U(x,t)')
plt.title('Эволюция температуры во времени')
plt.grid(True, alpha=0.3)
plt.legend()
# 1.3. Временная эволюция в характерных точках
plt.subplot(2, 2, 3)
x_points = [np.pi/8, np.pi/4, 3*np.pi/8, np.pi/2]
t_evolution = np.linspace(0, 10, 100)
for x_point in x_points:
temp_evolution = [self.analytical_solution(np.array([x_point]), t)[0]
for t in t_evolution]
plt.plot(t_evolution, temp_evolution, linewidth=2,
label=f'x = {x_point:.3f}')
plt.xlabel('Время t')
plt.ylabel('Температура U(x,t)')
plt.title('Эволюция температуры в точках')
plt.grid(True, alpha=0.3)
plt.legend()
# 1.4. Амплитуда установившихся колебаний
plt.subplot(2, 2, 4)
t_steady = np.linspace(8, 10, 100) # Установившийся режим
x_max_amp = np.pi/8 # Точка максимальной амплитуды
u_steady = [self.analytical_solution(np.array([x_max_amp]), t)[0]
for t in t_steady]
source_steady = [self.heat_source(np.array([x_max_amp]), t)[0]
for t in t_steady]
plt.plot(t_steady, u_steady, 'b-', linewidth=2, label='Температура')
plt.plot(t_steady, source_steady, 'r--', linewidth=2, label='Источник тепла')
plt.xlabel('Время t')
plt.ylabel('Значение')
plt.title('Установившиеся колебания (t > 5)')
plt.grid(True, alpha=0.3)
plt.legend()
plt.suptitle('Решение неоднородного уравнения теплопроводности', fontsize=16)
plt.tight_layout()
comparison_path = "results/images/solution_comparison.png"
plt.savefig(comparison_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['solution_comparison'] = comparison_path
# 2. Поверхность U(x,t) в пространстве
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
X, T = np.meshgrid(x, np.linspace(0, 10, 50))
U = np.zeros_like(X)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
U[i, j] = self.analytical_solution(X[i, j], T[i, j])
surf = ax.plot_surface(X, T, U, cmap='hot', alpha=0.8)
ax.set_xlabel('x')
ax.set_ylabel('t')
ax.set_zlabel('U(x,t)')
ax.set_title('Поверхность распределения температуры U(x,t)', fontsize=14)
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)
surface_path = "results/images/temperature_surface.png"
plt.savefig(surface_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['temperature_surface'] = surface_path
# 3. Анимация распространения тепла
self.create_temperature_animation(x, visualization_paths)
# 4. Анализ переходного процесса
self.create_transient_analysis(x, visualization_paths)
# 5. Сравнение с однородным случаем
self.create_homogeneous_comparison(x, visualization_paths)
except Exception as e:
print(f"Ошибка при создании визуализаций: {e}")
return visualization_paths
def create_temperature_animation(self, x: np.ndarray, visualization_paths: Dict[str, str]):
"""Создание анимации распространения тепла"""
try:
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 8))
# Время для анимации
t_anim = np.linspace(0, 10, 100)
# Настройка графиков
ax1.set_xlim(0, self.L)
ax1.set_ylim(-15, 15)
ax1.set_xlabel('x')
ax1.set_ylabel('U(x,t)')
ax1.grid(True, alpha=0.3)
ax2.set_xlim(0, self.L)
ax2.set_ylim(-15, 15)
ax2.set_xlabel('x')
ax2.set_ylabel('Источник тепла')
ax2.grid(True, alpha=0.3)
# Первый кадр
line_temp, = ax1.plot(x, self.analytical_solution(x, 0), 'b-', linewidth=2, label='Температура')
line_source, = ax2.plot(x, self.heat_source(x, 0), 'r-', linewidth=2, label='Источник тепла')
ax1.legend()
ax2.legend()
def animate(i):
t = t_anim[i]
# Вычисляем решения
u = self.analytical_solution(x, t)
source = self.heat_source(x, t)
# Обновляем графики
line_temp.set_ydata(u)
line_source.set_ydata(source)
ax1.set_title(f'Распределение температуры, t = {t:.2f}')
ax2.set_title(f'Распределение источника тепла, t = {t:.2f}')
return line_temp, line_source
anim = animation.FuncAnimation(fig, animate, frames=len(t_anim),
interval=50, blit=True)
# Сохраняем анимацию
animation_path = "results/images/temperature_animation.gif"
anim.save(animation_path, writer='pillow', fps=20)
plt.close()
visualization_paths['temperature_animation'] = animation_path
print("Анимация распространения тепла создана!")
except Exception as e:
print(f"Ошибка при создании анимации: {e}")
def create_transient_analysis(self, x: np.ndarray, visualization_paths: Dict[str, str]):
"""Анализ переходного процесса"""
try:
plt.figure(figsize=(12, 8))
# 1. Временные составляющие решения
plt.subplot(2, 2, 1)
t_analysis = np.linspace(0, 5, 100)
transient = -np.exp(-t_analysis)
oscillatory = np.cos(3*t_analysis) + 3*np.sin(3*t_analysis)
total = transient + oscillatory
plt.plot(t_analysis, transient, 'r-', linewidth=2, label='Переходная составляющая')
plt.plot(t_analysis, oscillatory, 'g-', linewidth=2, label='Колебательная составляющая')
plt.plot(t_analysis, total, 'b-', linewidth=2, label='Полное решение')
plt.xlabel('Время t')
plt.ylabel('Амплитуда')
plt.title('Временные составляющие решения')
plt.grid(True, alpha=0.3)
plt.legend()
# 2. Затухание переходной составляющей
plt.subplot(2, 2, 2)
t_decay = np.linspace(0, 3, 100)
transient_decay = -np.exp(-t_decay)
plt.semilogy(t_decay, np.abs(transient_decay), 'r-', linewidth=2)
plt.xlabel('Время t')
plt.ylabel('|Переходная составляющая|')
plt.title('Затухание переходной составляющей')
plt.grid(True, alpha=0.3)
# 3. Фазовый портрет установившихся колебаний
plt.subplot(2, 2, 3)
t_phase = np.linspace(8, 10, 1000)
u_steady = np.cos(3*t_phase) + 3*np.sin(3*t_phase)
u_steady_deriv = -3*np.sin(3*t_phase) + 9*np.cos(3*t_phase)
plt.plot(u_steady, u_steady_deriv, 'b-', linewidth=1)
plt.xlabel('U(t)')
plt.ylabel('dU/dt')
plt.title('Фазовый портрет установившихся колебаний')
plt.grid(True, alpha=0.3)
# 4. Спектральный анализ
plt.subplot(2, 2, 4)
components = self.calculate_solution_components()
frequencies = [0, 3] # Постоянная составляющая и частота 3
amplitudes = [components['transient']['decay_rate'],
components['steady_oscillatory']['amplitude']]
plt.stem(frequencies, amplitudes, basefmt=' ')
plt.xlabel('Частота')
plt.ylabel('Амплитуда')
plt.title('Спектральный состав решения')
plt.grid(True, alpha=0.3)
plt.suptitle('Анализ переходного процесса', fontsize=16)
plt.tight_layout()
transient_path = "results/images/transient_analysis.png"
plt.savefig(transient_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['transient_analysis'] = transient_path
except Exception as e:
print(f"Ошибка при анализе переходного процесса: {e}")
def create_homogeneous_comparison(self, x: np.ndarray, visualization_paths: Dict[str, str]):
"""Сравнение с однородным случаем"""
try:
plt.figure(figsize=(12, 6))
t_comparison = [0.1, 1.0, 5.0]
for i, t in enumerate(t_comparison):
plt.subplot(1, 3, i+1)
u_nonhomogeneous = self.analytical_solution(x, t)
u_homogeneous = self.homogeneous_solution(x, t)
plt.plot(x, u_nonhomogeneous, 'b-', linewidth=2, label='Неоднородное уравнение')
plt.plot(x, u_homogeneous, 'r--', linewidth=2, label='Однородное уравнение')
plt.plot(x, self.heat_source(x, t), 'g:', linewidth=1, label='Источник тепла')
plt.xlabel('x')
plt.ylabel('U(x,t)')
plt.title(f'Сравнение при t = {t}')
plt.grid(True, alpha=0.3)
plt.legend()
plt.suptitle('Сравнение решений неоднородного и однородного уравнений', fontsize=14)
plt.tight_layout()
comparison_path = "results/images/homogeneous_comparison.png"
plt.savefig(comparison_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['homogeneous_comparison'] = comparison_path
except Exception as e:
print(f"Ошибка при сравнении с однородным случаем: {e}")
def calculate_temperature_table(self) -> List[List[Any]]:
"""Вычисление таблицы температур в характерных точках"""
table_data = []
# Характерные точки и моменты времени
x_points = [np.pi/8, np.pi/4, np.pi/2, 3*np.pi/4, 7*np.pi/8]
t_points = [0, 0.5, 1.0, 2.0, 5.0, 10.0]
for x in x_points:
for t in t_points:
temperature = self.analytical_solution(np.array([x]), t)[0]
heat_source_val = self.heat_source(np.array([x]), t)[0]
table_data.append([
f"{x:.3f}", f"{t:.1f}",
f"{temperature:.6f}", f"{heat_source_val:.6f}"
])
return table_data
def analyze(self):
"""Выполнение полного анализа неоднородного уравнения теплопроводности"""
print("Решение неоднородного уравнения теплопроводности методом Фурье...")
# Вычисление параметров решения
components = self.calculate_solution_components()
print("Создание визуализаций...")
visualizations = self.create_visualizations()
print("Вычисление таблицы температур...")
temperature_table = self.calculate_temperature_table()
# Физический анализ
physical_analysis = self.physical_analysis()
# Математический анализ метода
mathematical_analysis = self.mathematical_analysis()
# Сохранение результатов
self.results = {
'components': components,
'visualizations': visualizations,
'temperature_table': temperature_table,
'physical_analysis': physical_analysis,
'mathematical_analysis': mathematical_analysis,
'problem_definition': {
'equation': self.equation,
'initial_condition': self.initial_condition,
'boundary_conditions': self.boundary_conditions,
'domain': self.domain
},
'analytical_solution': {
'formula': "U(x,t) = [-exp(-t) + cos(3t) + 3sin(3t)] · sin(4x)",
'interpretation': "Решение представляет собой затухающую экспоненту плюс установившиеся колебания, умноженные на пространственную моду sin(4x)"
}
}
return self.results
def physical_analysis(self) -> Dict[str, Any]:
"""Физический анализ решения"""
# Анализ установившегося режима
t_steady = 10.0 # Время, когда переходный процесс завершился
x_test = np.pi/8 # Точка для анализа
u_steady = self.analytical_solution(np.array([x_test]), t_steady)[0]
source_steady = self.heat_source(np.array([x_test]), t_steady)[0]
# Энергетический анализ
x_energy = np.linspace(0, self.L, 1000)
u_energy = self.analytical_solution(x_energy, t_steady)
energy = np.trapezoid(u_energy**2, x_energy)
return {
'steady_state_amplitude': np.sqrt(1**2 + 3**2), # sqrt(cos² + sin²)
'phase_shift': np.arctan2(3, 1),
'resonance_frequency': 4, # Пространственная частота источника
'energy_steady_state': energy,
'physical_interpretation': 'Система совершает вынужденные колебания под действием периодического источника тепла'
}
def mathematical_analysis(self) -> Dict[str, Any]:
"""Математический анализ метода решения"""
return {
'method': 'Разложение по собственным функциям',
'eigenfunctions': 'sin(nx), n=1,2,3,...',
'eigenvalues': 'n²/16',
'particular_solution_method': 'Метод неопределенных коэффициентов',
'boundary_conditions_satisfied': True,
'initial_condition_satisfied': True,
'convergence': 'Быстрая сходимость благодаря резонансу с 4-й гармоникой'
}
def get_analysis_description(self):
"""Возвращает описание анализа и методики"""
description = {
'title': "Решение смешанной задачи для неоднородного уравнения теплопроводности",
'discipline': "СПЕЦИАЛЬНЫЕ ГЛАВЫ МАТЕМАТИКИ",
'topic': "Решение неоднородного уравнения теплопроводности методом Фурье",
'variant': "Вариант 6",
'purpose': "Изучение методов решения смешанной задачи для неоднородного уравнения теплопроводности методом Фурье с использованием метода разложения по собственным функциям",
'tasks': [
"Аналитическое решение методом разделения переменных",
"Решение неоднородного уравнения методом разложения по собственным функциям",
"Анализ переходных и установившихся процессов",
"Исследование влияния источника тепла на распределение температуры",
"Сравнение с решением однородного уравнения"
],
'methodology': {
'separation_of_variables': "Метод разделения переменных для неоднородного уравнения",
'eigenfunction_expansion': "Разложение решения и правой части по собственным функциям",
'particular_solution': "Метод неопределенных коэффициентов для нахождения частного решения",
'transient_analysis': "Анализ переходных и установившихся процессов"
},
'problem': {
'equation': self.equation,
'initial_condition': self.initial_condition,
'boundary_conditions': self.boundary_conditions,
'domain': self.domain
}
}
return description
class NonhomogeneousHeatEquationMarkdownReport:
"""Класс для генерации полного отчета в Markdown"""
def __init__(self, analyzer: NonhomogeneousHeatEquationAnalyzer, analysis_results: Dict[str, Any]):
self.analyzer = analyzer
self.results = analysis_results
def add_header(self, title: str, level: int = 1) -> str:
return f"{'#' * level} {title}\n\n"
def add_table(self, data: List[List[Any]], headers: List[str], title: str = "") -> str:
table_str = ""
if title:
table_str += f"**{title}**\n\n"
table_str += "| " + " | ".join(headers) + " |\n"
table_str += "|" + "|".join(["---"] * len(headers)) + "|\n"
for row in data:
table_str += "| " + " | ".join(map(str, row)) + " |\n"
table_str += "\n"
return table_str
def add_image(self, image_path: str, caption: str = "") -> str:
if os.path.exists(image_path):
return (f'<div align="center">\n\n'
f'<img src="{image_path}" alt="{caption}" style="max-width: 80%; height: auto; border: 1px solid #ddd; padding: 5px; background: #f8f9fa;">\n\n'
f'**Рисунок:** {caption}\n\n'
f'</div>\n\n')
else:
return f"*Изображение не найдено: {caption}*\n\n"
def add_code_section(self) -> str:
success, src = read_own_source()
section = self.add_header("ПРИЛОЖЕНИЕ А", 2)
section += "**Исходный код программы**\n\n"
if success:
section += "```python\n" + src
if not src.endswith("\n"):
section += "\n"
section += "```\n"
else:
section += f"*Не удалось прочитать исходный код: {src}*\n"
return section
def generate_report(self) -> str:
report = ""
# Титульная страница
report += '<div style="page-break-after: always;">\n\n'
report += "# Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования\n\n"
report += "### «Казанский национальный исследовательский технологический университет»\n\n"
report += "#### Институт: Институт управления, автоматизации и информационных технологий\n"
report += "#### Кафедра Информатики и прикладной математики\n\n"
report += "---\n\n"
report += "# ЛАБОРАТОРНАЯ РАБОТА\n\n"
description = self.analyzer.get_analysis_description()
report += f"### по дисциплине: «{description['discipline']}»\n\n"
report += f"### на тему: «{description['topic']}»\n\n"
report += f"### {description['variant']}\n\n"
report += "---\n\n"
report += "**Выполнил:** \n"
report += "студент группы 851-М81 \n"
report += "Меркулов А. Д. \n"
report += '</div>\n\n'
# Содержание
report += self.add_header("СОДЕРЖАНИЕ", 1)
toc = [
"1. ВВЕДЕНИЕ",
"2. ПОСТАНОВКА ЗАДАЧИ",
"3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ",
" 3.1. Метод разделения переменных для неоднородного уравнения",
" 3.2. Разложение по собственным функциям",
"4. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ",
" 4.1. Метод решения",
" 4.2. Окончательное решение",
"5. ФИЗИЧЕСКИЙ АНАЛИЗ",
" 5.1. Переходные процессы",
" 5.2. Установившиеся колебания",
" 5.3. Влияние источника тепла",
"6. МАТЕМАТИЧЕСКИЙ АНАЛИЗ",
"7. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ",
"8. ВЫВОДЫ",
"ПРИЛОЖЕНИЕ А"
]
for item in toc:
report += f"{item}\n\n"
report += "---\n\n"
# 1) Введение
report += self.add_header("1. ВВЕДЕНИЕ", 1)
report += f"**Цель работы:** {description['purpose']}\n\n"
report += "**Задачи исследования:**\n"
for i, task in enumerate(description['tasks'], 1):
report += f"{i}. {task}\n"
report += "\n"
report += "**Актуальность исследования** обусловлена важностью неоднородных уравнений теплопроводности в практических приложениях. Такие уравнения описывают процессы теплопередачи с внутренними источниками тепла, что характерно для многих инженерных систем, биологических процессов и технологических установок.\n\n"
# 2) Постановка задачи
report += self.add_header("2. ПОСТАНОВКА ЗАДАЧИ", 1)
problem_def = description['problem']
report += f"**Неоднородное уравнение теплопроводности:** {problem_def['equation']}\n\n"
report += f"**Начальное условие:** {problem_def['initial_condition']}\n\n"
report += f"**Граничные условия:** {problem_def['boundary_conditions']}\n\n"
report += f"**Область определения:** {problem_def['domain']}\n\n"
report += "**Физическая интерпретация:** Рассматривается задача о распределении температуры в стержне с внутренним источником тепла, который совершает гармонические колебания во времени и пространстве. Концы стержня поддерживаются при нулевой температуре.\n\n"
# 3) Теоретические основы
report += self.add_header("3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ", 1)
report += self.add_header("3.1. Метод разделения переменных для неоднородного уравнения", 2)
methodology = description['methodology']
report += f"**{list(methodology.keys())[0]}:** {methodology['separation_of_variables']}\n\n"
report += "Для неоднородного уравнения теплопроводности:\n"
report += "U_t = aU_xx + f(x,t)\n\n"
report += "Решение ищется в виде разложения по собственным функциям:\n"
report += "U(x,t) = Σₙ Tₙ(t) Xₙ(x)\n\n"
report += self.add_header("3.2. Разложение по собственным функциям", 2)
report += f"**{list(methodology.keys())[1]}:** {methodology['eigenfunction_expansion']}\n\n"
report += f"**{list(methodology.keys())[2]}:** {methodology['particular_solution']}\n\n"
report += "Собственные функции для граничных условий U(0,t)=U(π,t)=0:\n"
report += "Xₙ(x) = sin(nx), λₙ = n²\n\n"
# 4) Аналитическое решение
report += self.add_header("4. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ", 1)
analytical = self.results['analytical_solution']
components = self.results['components']
report += self.add_header("4.1. Метод решения", 2)
report += "1. Разложение правой части по собственным функциям:\n"
report += " f(x,t) = 10cos(3t)sin(4x) = f₄(t)sin(4x)\n"
report += " где f₄(t) = 10cos(3t)\n\n"
report += "2. Уравнение для временных коэффициентов:\n"
report += " T₄'(t) + (4²/16)T₄(t) = 10cos(3t)\n"
report += " T₄'(t) + T₄(t) = 10cos(3t)\n\n"
report += "3. Решение однородного уравнения:\n"
report += " T₄ʰ(t) = Cexp(-t)\n\n"
report += "4. Частное решение неоднородного уравнения:\n"
report += " T₄ᵖ(t) = Acos(3t) + Bsin(3t)\n\n"
report += self.add_header("4.2. Окончательное решение", 2)
report += f"**Аналитическое решение:** {analytical['formula']}\n\n"
report += f"**Физическая интерпретация:** {analytical['interpretation']}\n\n"
report += "**Составляющие решения:**\n"
report += f"- Переходная составляющая: {components['transient']['description']}\n"
report += f"- Установившиеся колебания: {components['steady_oscillatory']['description']}\n"
report += f"- Пространственное распределение: {components['spatial']['description']}\n\n"
# 5) Физический анализ
report += self.add_header("5. ФИЗИЧЕСКИЙ АНАЛИЗ", 1)
physical = self.results['physical_analysis']
mathematical = self.results['mathematical_analysis']
report += self.add_header("5.1. Переходные процессы", 2)
report += "Переходный процесс характеризуется экспоненциальным затуханием:\n"
report += "- Время затухания: 1/λ = 1 единица времени\n"
report += "- Полное затухание через 3-5 единиц времени\n\n"
report += self.add_header("5.2. Установившиеся колебания", 2)
report += f"**Амплитуда установившихся колебаний:** {physical['steady_state_amplitude']:.4f}\n"
report += f"**Фазовый сдвиг:** {physical['phase_shift']:.4f} радиан\n"
report += f"**Резонансная частота:** {physical['resonance_frequency']}\n\n"
report += self.add_header("5.3. Влияние источника тепла", 2)
report += "- Источник тепла создает вынужденные колебания температуры\n"
report += "- Система резонирует с пространственной гармоникой sin(4x)\n"
report += "- Энергия системы в установившемся режиме постоянна\n\n"
# 6) Математический анализ
report += self.add_header("6. МАТЕМАТИЧЕСКИЙ АНАЛИЗ", 1)
report += f"**Метод решения:** {mathematical['method']}\n\n"
report += f"**Собственные функции:** {mathematical['eigenfunctions']}\n\n"
report += f"**Собственные значения:** {mathematical['eigenvalues']}\n\n"
report += f"**Метод частного решения:** {mathematical['particular_solution_method']}\n\n"
report += f"**Выполнение граничных условий:** {'Да' if mathematical['boundary_conditions_satisfied'] else 'Нет'}\n\n"
report += f"**Выполнение начального условия:** {'Да' if mathematical['initial_condition_satisfied'] else 'Нет'}\n\n"
# 7) Визуализация результатов
report += self.add_header("7. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ", 1)
visualizations = self.results['visualizations']
# Таблица температур
table_data = self.results['temperature_table'][:10] # Первые 10 строк
report += self.add_table(table_data, ["x", "t", "Температура U(x,t)", "Источник тепла"],
"Температура и источник тепла в характерных точках")
if 'solution_comparison' in visualizations:
report += self.add_image(visualizations['solution_comparison'],
"Сравнение решений и анализ установившихся колебаний")
if 'temperature_surface' in visualizations:
report += self.add_image(visualizations['temperature_surface'],
"Поверхность распределения температуры U(x,t)")
if 'transient_analysis' in visualizations:
report += self.add_image(visualizations['transient_analysis'],
"Анализ переходного процесса")
if 'homogeneous_comparison' in visualizations:
report += self.add_image(visualizations['homogeneous_comparison'],
"Сравнение с однородным уравнением")
if 'temperature_animation' in visualizations:
report += self.add_image(visualizations['temperature_animation'],
"Анимация распространения тепла в стержне")
report += "**Примечание:** Анимация демонстрирует переход от нулевого начального условия к установившимся колебаниям под действием источника тепла.\n\n"
# 8) Выводы
report += self.add_header("8. ВЫВОДЫ", 1)
conclusions = [
"Успешно решена смешанная задача для неоднородного уравнения теплопроводности",
"Получено аналитическое решение методом разложения по собственным функциям",
"Решение представляет собой суперпозицию затухающей экспоненты и установившихся колебаний",
"Установившиеся колебания имеют амплитуду √10 и фазовый сдвиг arctg(3)",
"Переходный процесс полностью затухает за 3-5 единиц времени",
"Система резонирует с пространственной гармоникой sin(4x)",
"Источник тепла создает периодические колебания температуры по всему стержню",
"Граничные и начальные условия выполняются точно",
"Визуализация подтвердила теоретические выводы о поведении решения"
]
for i, conclusion in enumerate(conclusions, 1):
report += f"{i}. {conclusion}\n"
report += "\n"
# Приложение
report += self.add_code_section()
return report
class NonhomogeneousHeatEquationDocxReport:
"""Класс для генерации отчета в формате DOCX"""
def __init__(self, analyzer: NonhomogeneousHeatEquationAnalyzer, analysis_results: Dict[str, Any]):
self.analyzer = analyzer
self.results = analysis_results
def setup_document_styles(self, doc):
"""Настройка стилей документа"""
try:
doc.styles['Normal'].font.name = 'Times New Roman'
doc.styles['Normal']._element.rPr.rFonts.set(qn('w:eastAsia'), 'Times New Roman')
doc.styles['Normal'].font.size = Pt(12)
except:
pass
def add_table_to_docx(self, doc, data: List[List[Any]], headers: List[str], title: str = ""):
"""Добавляет таблицу в DOCX документ"""
if title:
p = doc.add_paragraph()
p.add_run(title).bold = True
p.alignment = WD_ALIGN_PARAGRAPH.CENTER
doc.add_paragraph()
table = doc.add_table(rows=len(data)+1, cols=len(headers))
table.style = 'Table Grid'
# Заголовки
hdr_cells = table.rows[0].cells
for i, header in enumerate(headers):
hdr_cells[i].text = str(header)
hdr_cells[i].paragraphs[0].alignment = WD_ALIGN_PARAGRAPH.CENTER
for paragraph in hdr_cells[i].paragraphs:
for run in paragraph.runs:
run.bold = True
# Данные
for i, row in enumerate(data, 1):
row_cells = table.rows[i].cells
for j, cell in enumerate(row):
row_cells[j].text = str(cell)
if j > 0:
row_cells[j].paragraphs[0].alignment = WD_ALIGN_PARAGRAPH.CENTER
doc.add_paragraph()
def add_image_to_docx(self, doc, image_path: str, caption: str = ""):
"""Добавляет изображение в DOCX документ"""
if os.path.exists(image_path):
try:
paragraph = doc.add_paragraph()
paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
run = paragraph.add_run()
run.add_picture(image_path, width=Inches(5.0))
if caption:
caption_paragraph = doc.add_paragraph()
caption_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
caption_run = caption_paragraph.add_run(f"Рисунок: {caption}")
caption_run.italic = True
doc.add_paragraph()
except Exception as e:
doc.add_paragraph(f"Ошибка при добавлении изображения: {e}")
else:
doc.add_paragraph(f"Изображение не найдено: {caption}")
def generate_docx_report(self, filename: str = "nonhomogeneous_heat_equation_report.docx") -> str:
"""
Генерация отчёта в формате DOCX для неоднородного уравнения теплопроводности
"""
out_path = os.path.join("results", filename)
if not PYDOCX_AVAILABLE:
print("python-docx не установлен — DOCX отчёт не будет создан")
return out_path
try:
doc = Document()
self.setup_document_styles(doc)
# Титульная страница
title_paragraph = doc.add_paragraph()
title_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
title_run = title_paragraph.add_run("Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования\n«Казанский национальный исследовательский технологический университет»")
title_run.bold = True
title_run.font.size = Pt(14)
doc.add_paragraph()
university_paragraph = doc.add_paragraph()
university_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
university_paragraph.add_run("Институт: Институт управления, автоматизации и информационных технологий\nКафедра Информатики и прикладной математики").bold = True
doc.add_paragraph("\n" * 3)
# Название работы
work_paragraph = doc.add_paragraph()
work_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
work_run = work_paragraph.add_run("ЛАБОРАТОРНАЯ РАБОТA")
work_run.bold = True
work_run.font.size = Pt(16)
description = self.analyzer.get_analysis_description()
doc.add_paragraph()
discipline_paragraph = doc.add_paragraph()
discipline_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
discipline_paragraph.add_run(f"по дисциплине: «{description['discipline']}»").bold = True
doc.add_paragraph()
topic_paragraph = doc.add_paragraph()
topic_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
topic_paragraph.add_run(f"на тему: «{description['topic']}»").bold = True
doc.add_paragraph()
variant_paragraph = doc.add_paragraph()
variant_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
variant_paragraph.add_run(f"{description['variant']}").bold = True
doc.add_paragraph("\n" * 4)
# Информация о студенте
info_table = doc.add_table(rows=2, cols=2)
info_table.style = 'Table Grid'
info_table.cell(0, 0).text = "Выполнил:"
info_table.cell(0, 1).text = "студент группы 851-М81\nМеркулов А. Д."
for row in info_table.rows:
for cell in row.cells:
cell.paragraphs[0].alignment = WD_ALIGN_PARAGRAPH.LEFT
doc.add_page_break()
# Содержание
title = doc.add_paragraph()
title.alignment = WD_ALIGN_PARAGRAPH.CENTER
title.add_run("СОДЕРЖАНИЕ").bold = True
title.runs[0].font.size = Pt(14)
doc.add_paragraph()
toc_items = [
"1. ВВЕДЕНИЕ",
"2. ПОСТАНОВКА ЗАДАЧИ",
"3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ",
"4. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ",
"5. ФИЗИЧЕСКИЙ АНАЛИЗ",
"6. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ",
"7. ВЫВОДЫ",
"ПРИЛОЖЕНИЕ А"
]
for item in toc_items:
p = doc.add_paragraph()
p.add_run(item)
doc.add_page_break()
# Основное содержание
visualizations = self.results['visualizations']
analytical = self.results['analytical_solution']
# 1) Введение
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("1. ВВЕДЕНИЕ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
doc.add_paragraph(f"Цель работы: {description['purpose']}")
doc.add_paragraph("Задачи исследования:")
for task in description['tasks']:
p = doc.add_paragraph(task, style='List Bullet')
# 2) Постановка задачи
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("2. ПОСТАНОВКА ЗАДАЧИ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
problem_def = description['problem']
doc.add_paragraph(f"Неоднородное уравнение теплопроводности: {problem_def['equation']}")
doc.add_paragraph(f"Начальное условие: {problem_def['initial_condition']}")
doc.add_paragraph(f"Граничные условия: {problem_def['boundary_conditions']}")
doc.add_paragraph(f"Область определения: {problem_def['domain']}")
# 3) Теоретические основы
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
methodology = description['methodology']
doc.add_paragraph(f"Метод разделения переменных: {methodology['separation_of_variables']}")
doc.add_paragraph(f"Разложение по собственным функциям: {methodology['eigenfunction_expansion']}")
# 4) Аналитическое решение
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("4. АНАЛИТИЧЕСКОЕ РЕШЕНИЕ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
doc.add_paragraph(f"Аналитическое решение: {analytical['formula']}")
doc.add_paragraph(f"Физическая интерпретация: {analytical['interpretation']}")
# 5) Физический анализ
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("5. ФИЗИЧЕСКИЙ АНАЛИЗ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
physical = self.results['physical_analysis']
doc.add_paragraph(f"Амплитуда установившихся колебаний: {physical['steady_state_amplitude']:.4f}")
doc.add_paragraph(f"Резонансная частота: {physical['resonance_frequency']}")
# 6) Визуализация
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("6. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
if 'solution_comparison' in visualizations:
self.add_image_to_docx(doc, visualizations['solution_comparison'],
"Сравнение решений и анализ установившихся колебаний")
if 'temperature_surface' in visualizations:
self.add_image_to_docx(doc, visualizations['temperature_surface'],
"Поверхность распределения температуры")
if 'transient_analysis' in visualizations:
self.add_image_to_docx(doc, visualizations['transient_analysis'],
"Анализ переходного процесса")
# 7) Выводы
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("7. ВЫВОДЫ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
conclusions = [
"Получено аналитическое решение неоднородного уравнения теплопроводности",
"Исследованы переходные и установившиеся процессы",
"Проанализировано влияние источника тепла на распределение температуры",
"Визуализированы результаты решения"
]
for i, conclusion in enumerate(conclusions, 1):
doc.add_paragraph(f"{i}. {conclusion}", style='List Number')
# Приложение
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("ПРИЛОЖЕНИЕ А").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
subheading = doc.add_paragraph()
subheading.add_run("Исходный код программы").bold = True
success_src, src_text = read_own_source()
if success_src:
for line in src_text.splitlines():
p = doc.add_paragraph()
run = p.add_run(line)
try:
run.font.name = 'Courier New'
run.font.size = Pt(9)
except Exception:
pass
else:
doc.add_paragraph("Не удалось прочитать исходный код скрипта: " + src_text)
# Сохранение файла
doc.save(out_path)
print(f"DOCX-отчёт сохранён: {out_path}")
except Exception as e:
print(f"Ошибка при генерации DOCX-отчёта: {e}")
raise e
return out_path
def main():
"""Основная функция для выполнения лабораторной работы по неоднородному уравнению теплопроводности"""
# Создаем анализатор
analyzer = NonhomogeneousHeatEquationAnalyzer()
# Выполняем анализ
print("Решение неоднородного уравнения теплопроводности методом Фурье...")
results = analyzer.analyze()
# Создаем папку для результатов
os.makedirs("results", exist_ok=True)
os.makedirs("results/images", exist_ok=True)
# Генерируем Markdown отчет
md_reporter = NonhomogeneousHeatEquationMarkdownReport(analyzer, results)
md_report = md_reporter.generate_report()
# Сохраняем Markdown отчет
with open("README.md", "w", encoding="utf-8") as f:
f.write(md_report)
print("Markdown отчет сохранен: README.md")
# Генерируем DOCX отчет
docx_reporter = NonhomogeneousHeatEquationDocxReport(analyzer, results)
docx_path = docx_reporter.generate_docx_report()
# Выводим основные результаты в консоль
print("\n" + "="*80)
print("РЕЗУЛЬТАТЫ РЕШЕНИЯ НЕОДНОРОДНОГО УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ")
print("="*80)
analytical = results['analytical_solution']
components = results['components']
physical = results['physical_analysis']
print(f"\nАНАЛИТИЧЕСКОЕ РЕШЕНИЕ:")
print("-" * 50)
print(analytical['formula'])
print(f"\nСОСТАВЛЯЮЩИЕ РЕШЕНИЯ:")
print("-" * 50)
print(f"Переходная составляющая: {components['transient']['description']}")
print(f"Установившиеся колебания: {components['steady_oscillatory']['description']}")
print(f"Амплитуда колебаний: {components['steady_oscillatory']['amplitude']:.4f}")
print(f"\nФИЗИЧЕСКИЙ АНАЛИЗ:")
print("-" * 50)
print(f"Амплитуда установившихся колебаний: {physical['steady_state_amplitude']:.4f}")
print(f"Фазовый сдвиг: {physical['phase_shift']:.4f} радиан")
print(f"Резонансная частота: {physical['resonance_frequency']}")
print(f"\nВИЗУАЛИЗАЦИИ СОЗДАНЫ:")
print("-" * 50)
for name, path in results['visualizations'].items():
if os.path.exists(path):
print(f"✓ {name}: {path}")
print(f"\nОТЧЕТЫ СОХРАНЕНЫ:")
print("-" * 50)
print(f"✓ Markdown отчет: README.md")
if PYDOCX_AVAILABLE:
print(f"✓ DOCX отчет: {docx_path}")
return results
if __name__ == "__main__":
main()