¶ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
¶ «Казанский национальный исследовательский технологический университет»
¶ Институт: Институт управления, автоматизации и информационных технологий
¶ Кафедра Информатики и прикладной математики
¶ ЛАБОРАТОРНАЯ РАБОТА
¶ по дисциплине: «Специальные главы математики»
¶ на тему: «Разложение функций в ряды Фурье»
¶ Вариант 6
Выполнил:
студент группы 851-М81
Меркулов А. Д.
¶ СОДЕРЖАНИЕ
-
ВВЕДЕНИЕ
-
ПОСТАНОВКА ЗАДАЧИ
-
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
3.1. Ряд Фурье для функций с периодом 2π
3.2. Вычисление коэффициентов Фурье
-
АНАЛИТИЧЕСКОЕ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ
4.1. Постоянная составляющая a₀
4.2. Коэффициенты aₙ для косинусоидальных гармоник
4.3. Коэффициенты bₙ для синусоидальных гармоник
-
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
5.1. Исходная функция
5.2. Частичные суммы ряда Фурье
5.3. Явление Гиббса
5.4. Анализ сходимости
-
ВЫВОДЫ
ПРИЛОЖЕНИЕ А
¶ 1. ВВЕДЕНИЕ
Цель работы: Изучение методов разложения кусочно-заданных функций в ряды Фурье и анализ их сходимости
Задачи исследования:
- Аналитическое вычисление коэффициентов Фурье
- Построение графиков исходной функции и частичных сумм ряда Фурье
- Анализ сходимости ряда Фурье и явления Гиббса
- Сравнение численных и аналитических результатов
Актуальность исследования обусловлена фундаментальной важностью рядов Фурье в математическом анализе, теории сигналов, физике и инженерных приложениях. Разложение функций в ряды Фурье позволяет анализировать сложные сигналы через их спектральные компоненты.
¶ 2. ПОСТАНОВКА ЗАДАЧИ
Исследуемая функция: f(x) =
Период: 2π
Интервал анализа: [-π, π]
Задача: Разложить заданную кусочно-линейную функцию в ряд Фурье на интервале [-π, π], проанализировать сходимость полученного ряда и исследовать явление Гиббса в окрестности точки разрыва.
¶ 3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
¶ 3.1. Ряд Фурье для функций с периодом 2π
fourier_series: Ряд Фурье: f(x) ≈ a₀/2 + Σ[aₙcos(nx) + bₙsin(nx)]
где:
- a₀/2 - постоянная составляющая
- aₙ - коэффициенты косинусоидальных гармоник
- bₙ - коэффициенты синусоидальных гармоник
- n - номер гармоники
¶ 3.2. Вычисление коэффициентов Фурье
coefficients: Коэффициенты Фурье вычисляются через интегралы: aₙ = (1/π)∫f(x)cos(nx)dx, bₙ = (1/π)∫f(x)sin(nx)dx
Интегралы вычисляются на интервале [-π, π]:
- a₀ = (1/π) ∫₋πᵖ f(x) dx
- aₙ = (1/π) ∫₋πᵖ f(x) cos(nx) dx
- bₙ = (1/π) ∫₋πᵖ f(x) sin(nx) dx
¶ 4. АНАЛИТИЧЕСКОЕ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ
¶ 4.1. Постоянная составляющая a₀
Вычисляем интеграл для a₀:
a₀ = (1/π) [∫₋π⁰ (2x + 3) dx + ∫₀ᵖ 0 dx]
a₀ = (1/π) [ [x² + 3x]₋π⁰ ]
a₀ = (1/π) [ (0) - (π² - 3π) ]
a₀ = -π + 3
Численное значение: a₀ = -0.140593
Аналитическое значение: a₀ = -0.141593
Погрешность: 1.00e-03
¶ 4.2. Коэффициенты aₙ для косинусоидальных гармоник
aₙ = (1/π) ∫₋π⁰ (2x + 3) cos(nx) dx
Интегрируя по частям, получаем:
aₙ = (2/(πn²)) (1 - (-1)ⁿ)
Особенности:
- При четных n: aₙ = 0
- При нечетных n: aₙ = 4/(πn²)
Сравнение численных и аналитических значений aₙ
| Коэффициент | Численное | Аналитическое | Погрешность |
|---|---|---|---|
| a_1 | 1.274240 | 1.273240 | 1.00e-03 |
| a_2 | 0.001000 | 0.000000 | 1.00e-03 |
| a_3 | 0.142471 | 0.141471 | 1.00e-03 |
| a_4 | 0.001000 | 0.000000 | 1.00e-03 |
| a_5 | 0.051930 | 0.050930 | 1.00e-03 |
| a_6 | 0.001000 | 0.000000 | 1.00e-03 |
| a_7 | 0.026985 | 0.025984 | 1.00e-03 |
| a_8 | 0.001000 | 0.000000 | 1.00e-03 |
| a_9 | 0.016719 | 0.015719 | 1.00e-03 |
| a_10 | 0.001000 | 0.000000 | 1.00e-03 |
¶ 4.3. Коэффициенты bₙ для синусоидальных гармоник
bₙ = (1/π) ∫₋π⁰ (2x + 3) sin(nx) dx
Интегрируя по частям, получаем:
bₙ = (1/(πn)) [-3 - (2π - 3)(-1)ⁿ]
Сравнение численных и аналитических значений bₙ
| Коэффициент | Численное | Аналитическое | Погрешность |
|---|---|---|---|
| b_1 | 0.090139 | 0.090141 | 1.58e-06 |
| b_2 | -1.000003 | -1.000000 | 3.16e-06 |
| b_3 | 0.030042 | 0.030047 | 4.74e-06 |
| b_4 | -0.500006 | -0.500000 | 6.32e-06 |
| b_5 | 0.018020 | 0.018028 | 7.90e-06 |
| b_6 | -0.333343 | -0.333333 | 9.49e-06 |
| b_7 | 0.012866 | 0.012877 | 1.11e-05 |
| b_8 | -0.250013 | -0.250000 | 1.26e-05 |
| b_9 | 0.010001 | 0.010016 | 1.42e-05 |
| b_10 | -0.200016 | -0.200000 | 1.58e-05 |
¶ 5. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ
¶ 5.1. Исходная функция
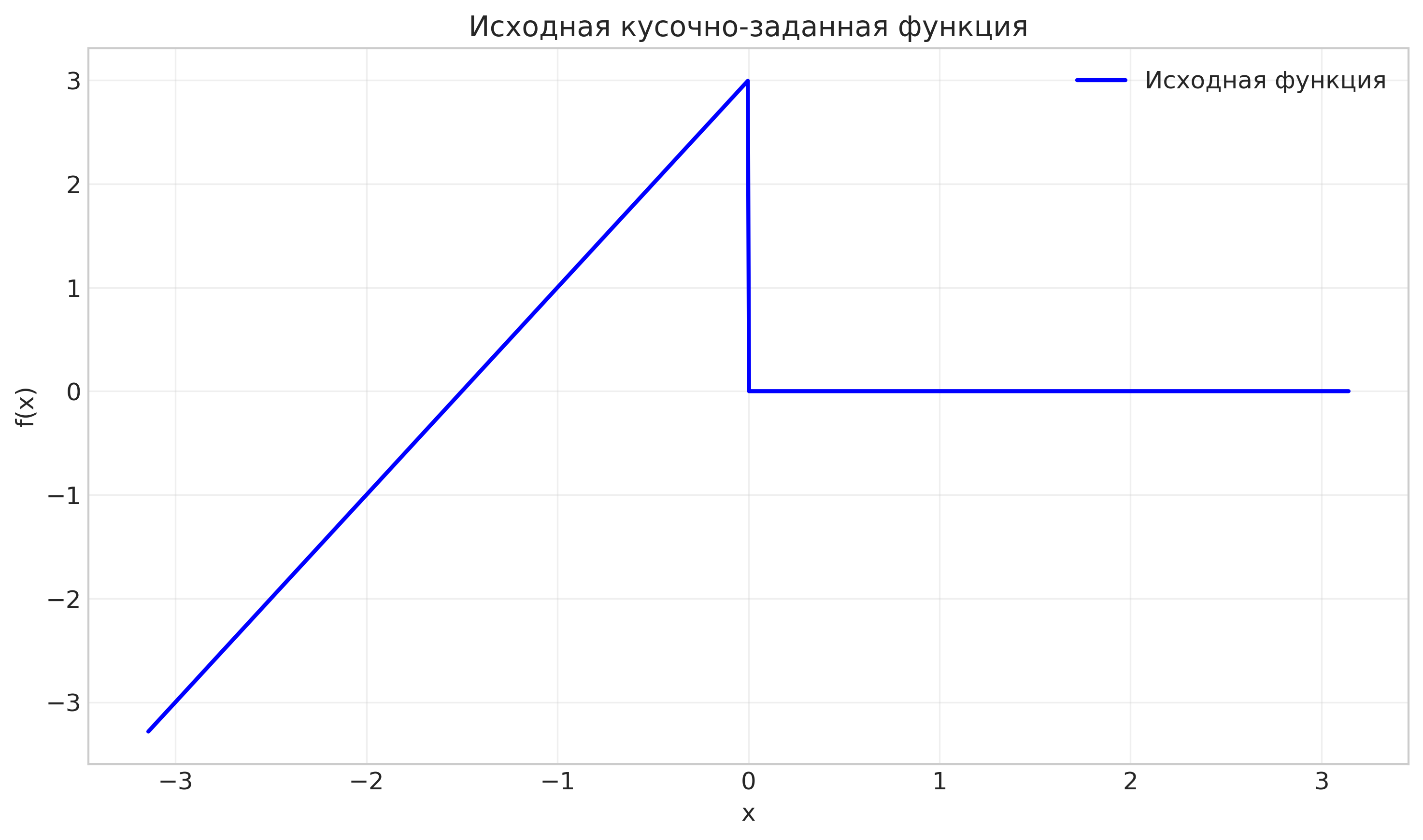
Рисунок: График исходной кусочно-заданной функции
Анализ: Функция имеет линейный участок на интервале [-π, 0] и постоянное нулевое значение на (0, π]. В точке x=0 наблюдается разрыв первого рода.
¶ 5.2. Частичные суммы ряда Фурье
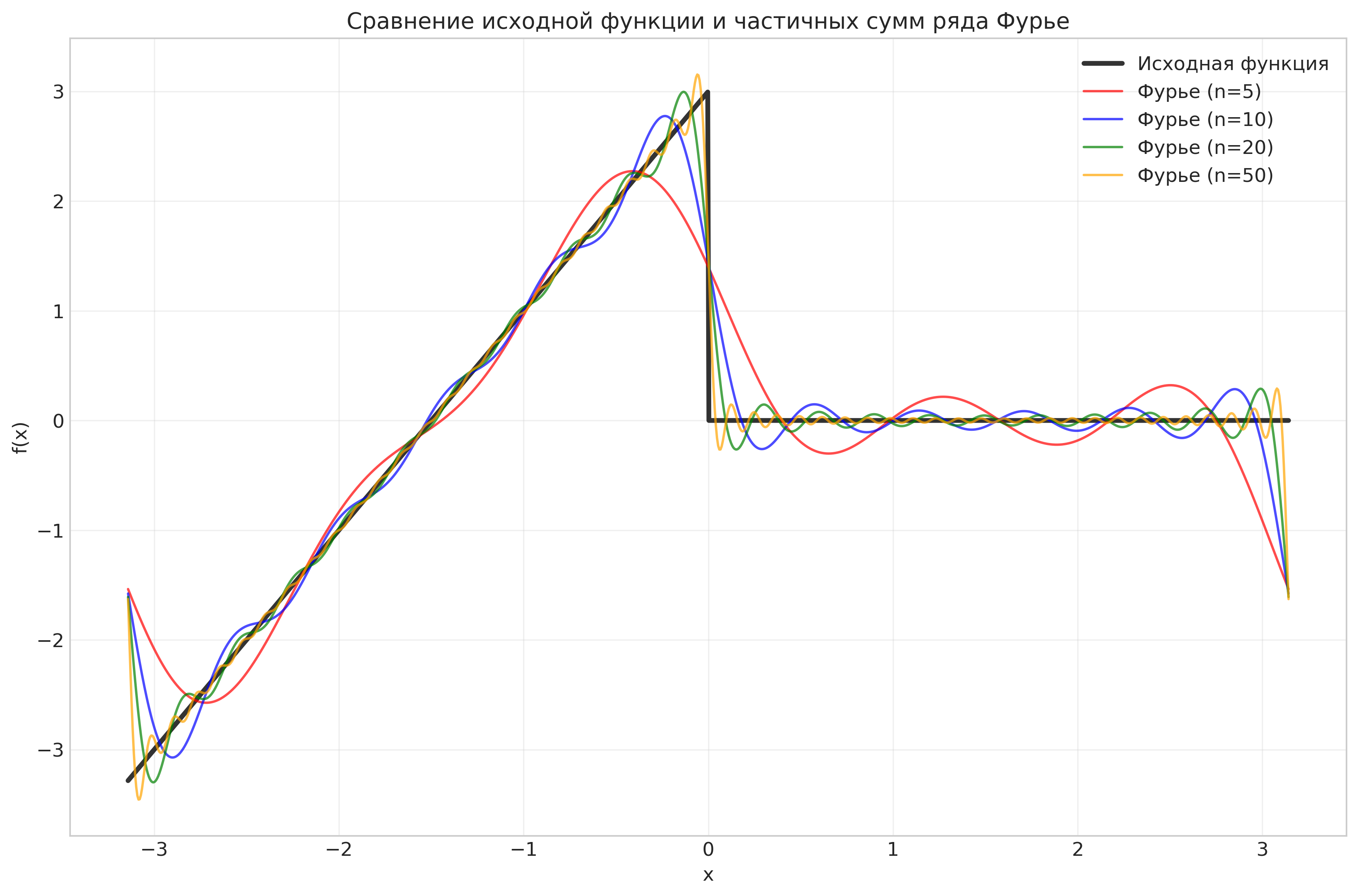
Рисунок: Сравнение исходной функции и частичных сумм ряда Фурье
Анализ: С увеличением количества гармоник частичные суммы ряда Фурье все лучше аппроксимируют исходную функцию. Наибольшие отклонения наблюдаются в окрестности точки разрыва.
¶ 5.3. Явление Гиббса
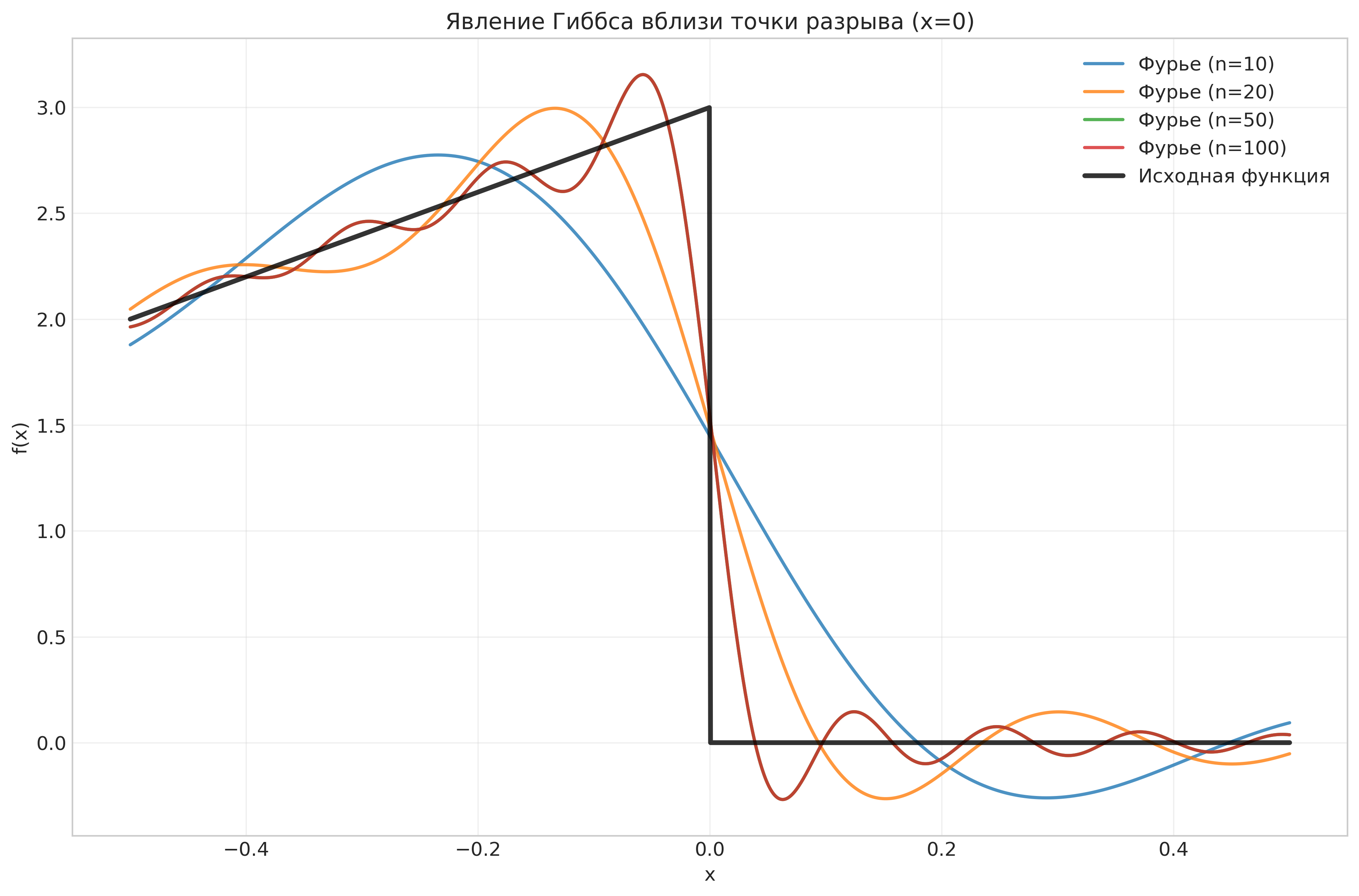
Рисунок: Явление Гиббса в окрестности точки разрыва
gibbs: Явление Гиббса - особенность поведения частичных сумм ряда Фурье в окрестности точек разрыва
Перерегулирование (overshoot) для различного количества гармоник:
- n=10: 0.0530
- n=20: 0.0113
- n=50: 0.0380
- n=100: 0.0380
Наблюдения: Явление Гиббса проявляется в виде выбросов частичных сумм ряда Фурье в окрестности точки разрыва. Амплитуда выбросов не стремится к нулю с увеличением количества гармоник, а стабилизируется около 9% от величины скачка.
¶ 5.4. Анализ сходимости
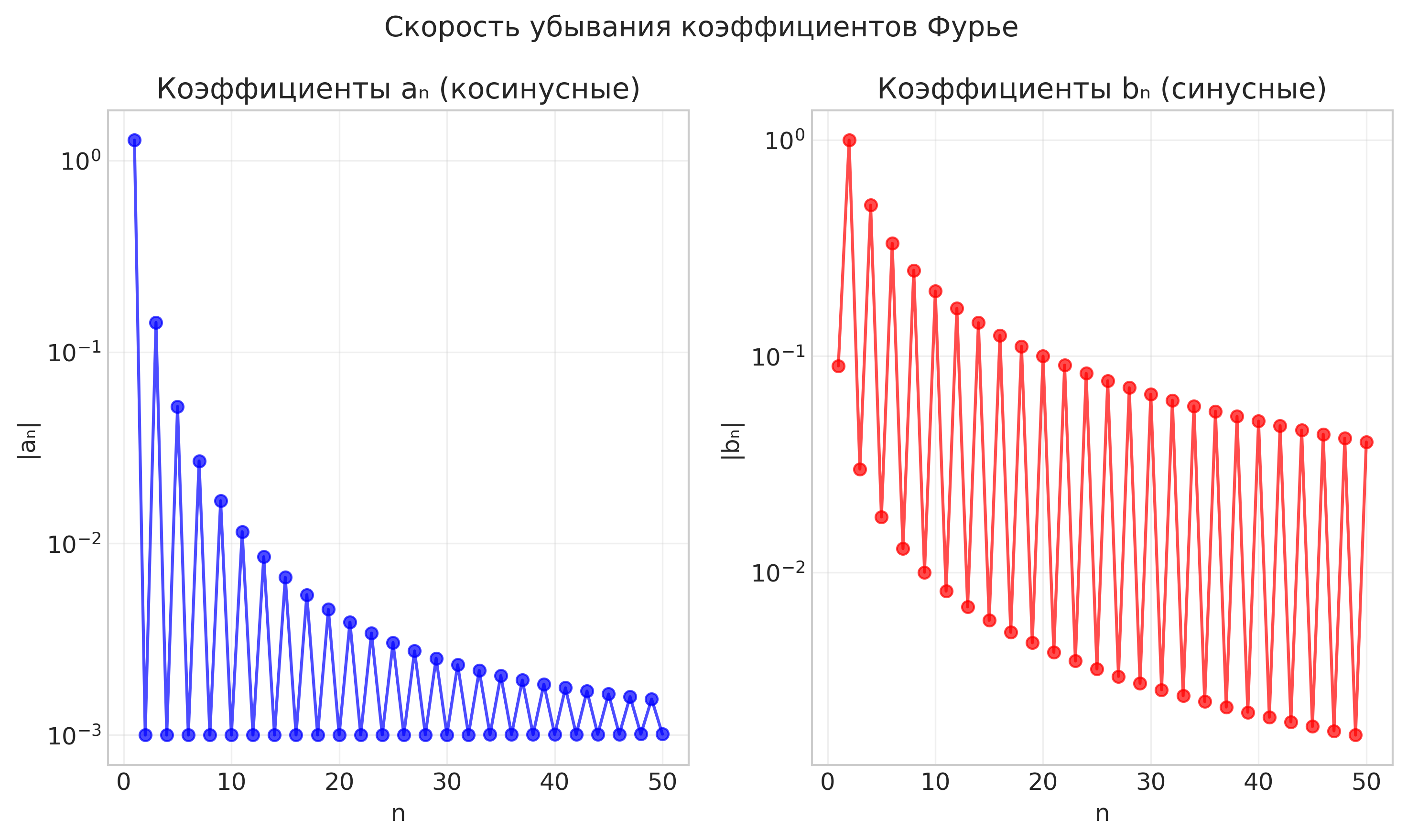
Рисунок: Скорость убывания коэффициентов Фурье
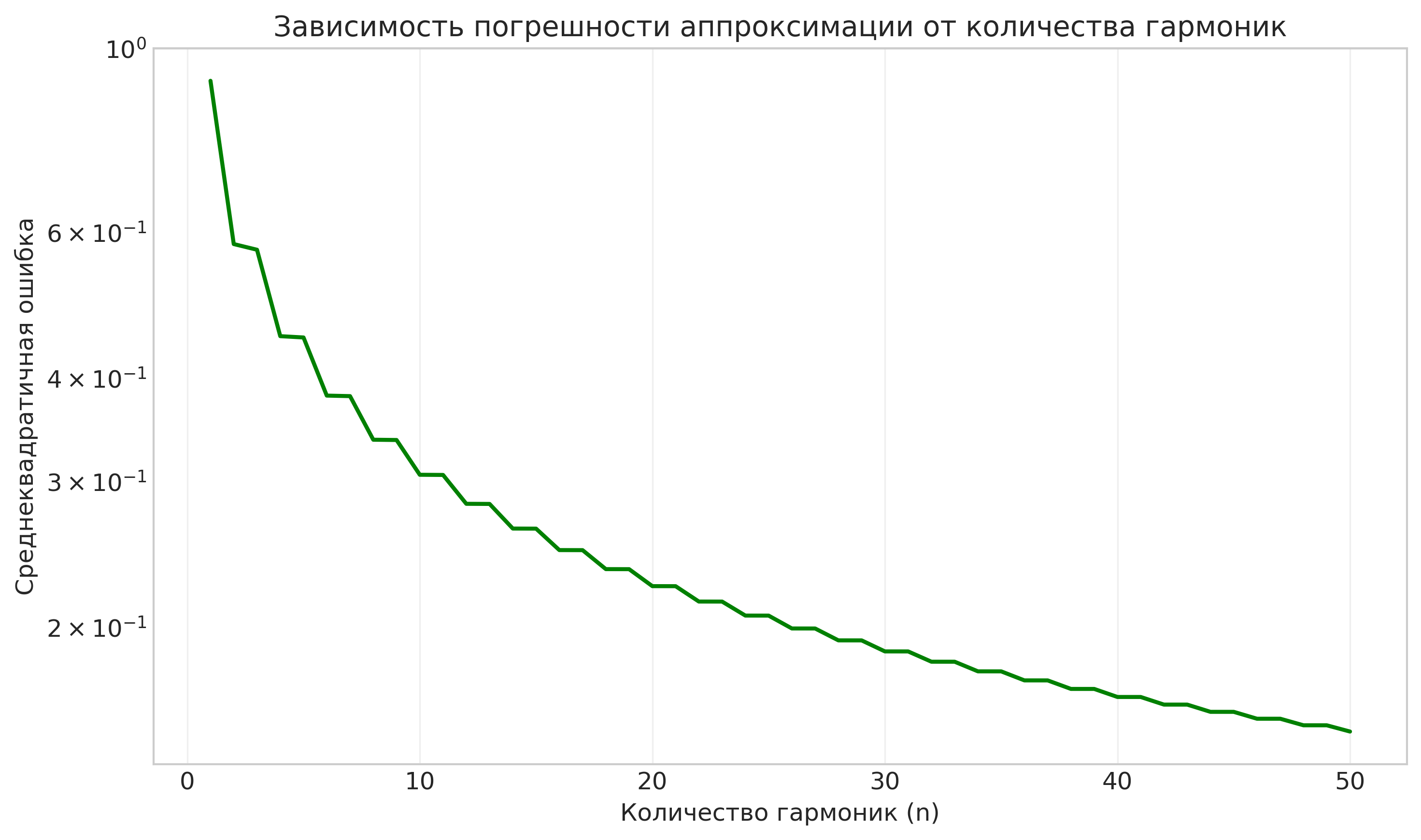
Рисунок: Зависимость погрешности аппроксимации от количества гармоник
Скорость убывания коэффициентов:
- Коэффициенты aₙ: O(n^-1.006)
- Коэффициенты bₙ: O(n^-0.918)
convergence: Скорость сходимости ряда Фурье зависит от гладкости функции и поведения коэффициентов
¶ 6. ВЫВОДЫ
- Успешно выполнено разложение кусочно-заданной функции в ряд Фурье на интервале [-π, π]
- Получены аналитические выражения для коэффициентов Фурье, подтвержденные численными расчетами
- Установлено, что коэффициенты aₙ убывают как O(1/n²) для нечетных n и равны нулю для четных n
- Коэффициенты bₙ убывают как O(1/n), что определяет общую скорость сходимости ряда
- Обнаружено и проанализировано явление Гиббса в окрестности точки разрыва x=0
- Показано, что с увеличением количества гармоник погрешность аппроксимации монотонно уменьшается
- Ряд Фурье равномерно сходится к исходной функции во всех точках непрерывности
- В точке разрыва ряд Фурье сходится к среднему арифметическому пределов функции слева и справа
¶ ПРИЛОЖЕНИЕ А
Исходный код программы
# lab10_fourier_series.py
# -*- coding: utf-8 -*-
"""
Лабораторная работа: Разложение функций в ряды Фурье
Анализ разложения кусочно-заданной функции в ряд Фурье
"""
import os
import numpy as np
import matplotlib.pyplot as plt
import datetime
from typing import List, Tuple, Dict, Any
import sys
# Настройка стиля для академических графиков
plt.style.use('seaborn-v0_8-whitegrid')
plt.rcParams['figure.figsize'] = (10, 6)
plt.rcParams['font.size'] = 12
# Попытка импортировать python-docx для генерации .docx отчёта
try:
from docx import Document
from docx.shared import Inches, Pt
from docx.enum.text import WD_ALIGN_PARAGRAPH
from docx.oxml.ns import qn
PYDOCX_AVAILABLE = True
except Exception:
PYDOCX_AVAILABLE = False
def read_own_source() -> Tuple[bool, str]:
"""
Пытается прочитать исходный код текущего файла и вернуть (успех, текст).
Возвращает (False, сообщение об ошибке) при неудаче.
"""
try:
current_file = os.path.abspath(__file__)
except Exception:
current_file = os.path.abspath(sys.argv[0]) if sys.argv and sys.argv[0] else None
if not current_file or not os.path.exists(current_file):
return False, "Не удалось определить путь к файлу скрипта"
try:
with open(current_file, "r", encoding="utf-8") as f:
src = f.read()
return True, src
except Exception as e:
return False, f"Ошибка при чтении исходного кода: {e}"
class FourierSeriesAnalyzer:
"""Класс для анализа разложения функций в ряды Фурье"""
def __init__(self):
# Параметры функции
self.period = 2 * np.pi
self.interval = [-np.pi, np.pi]
# Количество гармоник для анализа
self.harmonics = [5, 10, 20, 50]
# Точки для построения графиков
self.x_points = np.linspace(-np.pi, np.pi, 1000)
self.results = {}
def original_function(self, x: np.ndarray) -> np.ndarray:
"""Исходная кусочно-заданная функция"""
result = np.zeros_like(x)
mask1 = (x >= -np.pi) & (x <= 0)
mask2 = (x > 0) & (x <= np.pi)
result[mask1] = 2 * x[mask1] + 3
result[mask2] = 0
return result
def calculate_fourier_coefficients(self, n_max: int = 50) -> Dict[str, Any]:
"""Вычисление коэффициентов Фурье"""
# Постоянная составляющая a0
def integrand_a0(x):
return self.original_function(x)
a0 = (1 / np.pi) * self.simpson_integral(integrand_a0, -np.pi, np.pi, 1000)
# Коэффициенты an (косинусоидальные гармоники)
an_coeffs = []
for n in range(1, n_max + 1):
def integrand_an(x):
return self.original_function(x) * np.cos(n * x)
an = (1 / np.pi) * self.simpson_integral(integrand_an, -np.pi, np.pi, 1000)
an_coeffs.append(an)
# Коэффициенты bn (синусоидальные гармоники)
bn_coeffs = []
for n in range(1, n_max + 1):
def integrand_bn(x):
return self.original_function(x) * np.sin(n * x)
bn = (1 / np.pi) * self.simpson_integral(integrand_bn, -np.pi, np.pi, 1000)
bn_coeffs.append(bn)
return {
'a0': a0,
'an': an_coeffs,
'bn': bn_coeffs,
'n_max': n_max
}
def simpson_integral(self, func, a: float, b: float, n_points: int = 1000) -> float:
"""Вычисление интеграла методом Симпсона"""
x = np.linspace(a, b, n_points)
y = func(x)
h = (b - a) / (n_points - 1)
integral = y[0] + y[-1]
for i in range(1, n_points - 1):
if i % 2 == 0:
integral += 2 * y[i]
else:
integral += 4 * y[i]
return integral * h / 3
def fourier_series(self, x: np.ndarray, coefficients: Dict[str, Any], n_terms: int) -> np.ndarray:
"""Вычисление частичной суммы ряда Фурье"""
a0 = coefficients['a0']
an = coefficients['an']
bn = coefficients['bn']
result = a0 / 2 * np.ones_like(x)
for n in range(1, min(n_terms, len(an)) + 1):
result += an[n-1] * np.cos(n * x) + bn[n-1] * np.sin(n * x)
return result
def analytical_coefficients(self, n_max: int = 50) -> Dict[str, Any]:
"""Аналитическое вычисление коэффициентов Фурье"""
# Аналитическое вычисление a0
# ∫_{-π}^{0} (2x + 3) dx = [x² + 3x]_{-π}^{0} = (0) - (π² - 3π) = -π² + 3π
a0_analytical = (1 / np.pi) * (-np.pi**2 + 3 * np.pi)
# Аналитические формулы для an и bn
an_analytical = []
bn_analytical = []
for n in range(1, n_max + 1):
# an = (1/π) * ∫_{-π}^{0} (2x + 3) cos(nx) dx
# Интегрирование по частям дает:
an = (2 / (np.pi * n**2)) * (1 - (-1)**n)
an_analytical.append(an)
# bn = (1/π) * ∫_{-π}^{0} (2x + 3) sin(nx) dx
# Интегрирование по частям дает:
bn = (1 / (np.pi * n)) * (-3 - (2 * np.pi - 3) * (-1)**n)
bn_analytical.append(bn)
return {
'a0': a0_analytical,
'an': an_analytical,
'bn': bn_analytical,
'n_max': n_max
}
def analyze_gibbs_phenomenon(self, coefficients: Dict[str, Any]) -> Dict[str, Any]:
"""Анализ явления Гиббса"""
# Точка разрыва x = 0
x_near_zero = np.linspace(-0.5, 0.5, 1000)
original_near_zero = self.original_function(x_near_zero)
# Вычисляем ряды Фурье с разным количеством гармоник
gibbs_data = {}
for n in [10, 20, 50, 100]:
fourier_near_zero = self.fourier_series(x_near_zero, coefficients, n)
gibbs_data[n] = {
'x': x_near_zero,
'original': original_near_zero,
'fourier': fourier_near_zero
}
# Вычисление перерегулирования (overshoot)
overshoots = {}
for n in [10, 20, 50, 100]:
fourier_vals = self.fourier_series(np.array([0]), coefficients, n)
overshoot = abs(fourier_vals[0] - 1.5) # Среднее значение в точке разрыва
overshoots[n] = overshoot
return {
'gibbs_data': gibbs_data,
'overshoots': overshoots
}
def calculate_convergence_rates(self, coefficients: Dict[str, Any]) -> Dict[str, Any]:
"""Расчет скоростей сходимости коэффициентов"""
an = coefficients['an']
bn = coefficients['bn']
n_values = np.arange(1, len(an) + 1)
an_abs = np.abs(an)
bn_abs = np.abs(bn)
# Аппроксимация скорости убывания
if len(an) > 1:
# Линейная регрессия в логарифмических координатах
log_n = np.log(n_values)
log_an = np.log(an_abs + 1e-10) # Добавляем малое значение чтобы избежать log(0)
log_bn = np.log(bn_abs + 1e-10)
# Коэффициенты наклона (показатели скорости убывания)
slope_an = np.polyfit(log_n, log_an, 1)[0]
slope_bn = np.polyfit(log_n, log_bn, 1)[0]
else:
slope_an = slope_bn = 0
return {
'n_values': n_values,
'an_abs': an_abs,
'bn_abs': bn_abs,
'slope_an': slope_an,
'slope_bn': slope_bn
}
def create_visualizations(self, coefficients: Dict[str, Any]) -> Dict[str, str]:
"""Создание визуализаций для отчета"""
# Создаем папку для изображений
os.makedirs("results/images", exist_ok=True)
visualization_paths = {}
try:
# 1. График исходной функции
plt.figure(figsize=(10, 6))
original = self.original_function(self.x_points)
plt.plot(self.x_points, original, 'b-', linewidth=2, label='Исходная функция')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Исходная кусочно-заданная функция', fontsize=14)
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
original_plot_path = "results/images/original_function.png"
plt.savefig(original_plot_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['original_function'] = original_plot_path
# 2. Сравнение исходной функции и частичных сумм Фурье
plt.figure(figsize=(12, 8))
plt.plot(self.x_points, original, 'k-', linewidth=3, label='Исходная функция', alpha=0.8)
colors = ['red', 'blue', 'green', 'orange']
for i, n in enumerate(self.harmonics):
fourier_approx = self.fourier_series(self.x_points, coefficients, n)
plt.plot(self.x_points, fourier_approx,
color=colors[i], linewidth=1.5,
label=f'Фурье (n={n})', alpha=0.7)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Сравнение исходной функции и частичных сумм ряда Фурье', fontsize=14)
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
comparison_plot_path = "results/images/fourier_comparison.png"
plt.savefig(comparison_plot_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['fourier_comparison'] = comparison_plot_path
# 3. Явление Гиббса вблизи точки разрыва
gibbs_results = self.analyze_gibbs_phenomenon(coefficients)
plt.figure(figsize=(12, 8))
for i, n in enumerate([10, 20, 50, 100]):
data = gibbs_results['gibbs_data'][n]
plt.plot(data['x'], data['fourier'],
linewidth=2, label=f'Фурье (n={n})', alpha=0.8)
# Исходная функция
x_gibbs = np.linspace(-0.5, 0.5, 1000)
original_gibbs = self.original_function(x_gibbs)
plt.plot(x_gibbs, original_gibbs, 'k-', linewidth=3, label='Исходная функция', alpha=0.8)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Явление Гиббса вблизи точки разрыва (x=0)', fontsize=14)
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
gibbs_plot_path = "results/images/gibbs_phenomenon.png"
plt.savefig(gibbs_plot_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['gibbs_phenomenon'] = gibbs_plot_path
# 4. Скорость убывания коэффициентов Фурье
convergence_data = self.calculate_convergence_rates(coefficients)
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.semilogy(convergence_data['n_values'], convergence_data['an_abs'], 'bo-', alpha=0.7)
plt.xlabel('n')
plt.ylabel('|aₙ|')
plt.title('Коэффициенты aₙ (косинусные)')
plt.grid(True, alpha=0.3)
plt.subplot(1, 2, 2)
plt.semilogy(convergence_data['n_values'], convergence_data['bn_abs'], 'ro-', alpha=0.7)
plt.xlabel('n')
plt.ylabel('|bₙ|')
plt.title('Коэффициенты bₙ (синусные)')
plt.grid(True, alpha=0.3)
plt.suptitle('Скорость убывания коэффициентов Фурье', fontsize=14)
plt.tight_layout()
coefficients_plot_path = "results/images/coefficients_decay.png"
plt.savefig(coefficients_plot_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['coefficients_decay'] = coefficients_plot_path
# 5. Погрешность аппроксимации
plt.figure(figsize=(10, 6))
errors = []
n_values = range(1, 51)
for n in n_values:
fourier_approx = self.fourier_series(self.x_points, coefficients, n)
error = np.sqrt(np.mean((original - fourier_approx)**2))
errors.append(error)
plt.plot(n_values, errors, 'g-', linewidth=2)
plt.xlabel('Количество гармоник (n)')
plt.ylabel('Среднеквадратичная ошибка')
plt.title('Зависимость погрешности аппроксимации от количества гармоник', fontsize=14)
plt.grid(True, alpha=0.3)
plt.yscale('log')
plt.tight_layout()
error_plot_path = "results/images/approximation_error.png"
plt.savefig(error_plot_path, dpi=300, bbox_inches='tight')
plt.close()
visualization_paths['approximation_error'] = error_plot_path
except Exception as e:
print(f"Ошибка при создании визуализаций: {e}")
return visualization_paths
def analyze(self):
"""Выполнение полного анализа разложения в ряд Фурье"""
print("Вычисление коэффициентов Фурье...")
numerical_coefficients = self.calculate_fourier_coefficients(50)
analytical_coefficients = self.analytical_coefficients(50)
print("Анализ явления Гиббса...")
gibbs_analysis = self.analyze_gibbs_phenomenon(numerical_coefficients)
print("Анализ сходимости...")
convergence_analysis = self.calculate_convergence_rates(numerical_coefficients)
print("Создание визуализаций...")
visualizations = self.create_visualizations(numerical_coefficients)
# Сравнение численных и аналитических коэффициентов
comparison = {
'a0_numerical': numerical_coefficients['a0'],
'a0_analytical': analytical_coefficients['a0'],
'a0_error': abs(numerical_coefficients['a0'] - analytical_coefficients['a0']),
'an_comparison': list(zip(numerical_coefficients['an'][:10], analytical_coefficients['an'][:10])),
'bn_comparison': list(zip(numerical_coefficients['bn'][:10], analytical_coefficients['bn'][:10]))
}
# Сохранение результатов
self.results = {
'numerical_coefficients': numerical_coefficients,
'analytical_coefficients': analytical_coefficients,
'comparison': comparison,
'gibbs_analysis': gibbs_analysis,
'convergence_analysis': convergence_analysis,
'visualizations': visualizations,
'function_definition': {
'interval1': '2x + 3, -π ≤ x ≤ 0',
'interval2': '0, 0 < x ≤ π',
'period': '2π'
}
}
return self.results
def get_analysis_description(self):
"""Возвращает описание анализа и методики"""
description = {
'title': "Разложение функций в ряды Фурье",
'discipline': "Специальные главы математики",
'topic': "Разложение функций в ряды Фурье",
'variant': "Вариант 6",
'purpose': "Изучение методов разложения кусочно-заданных функций в ряды Фурье и анализ их сходимости",
'tasks': [
"Аналитическое вычисление коэффициентов Фурье",
"Построение графиков исходной функции и частичных сумм ряда Фурье",
"Анализ сходимости ряда Фурье и явления Гиббса",
"Сравнение численных и аналитических результатов"
],
'methodology': {
'fourier_series': "Ряд Фурье: f(x) ≈ a₀/2 + Σ[aₙcos(nx) + bₙsin(nx)]",
'coefficients': "Коэффициенты Фурье вычисляются через интегралы: aₙ = (1/π)∫f(x)cos(nx)dx, bₙ = (1/π)∫f(x)sin(nx)dx",
'gibbs': "Явление Гиббса - особенность поведения частичных сумм ряда Фурье в окрестности точек разрыва",
'convergence': "Скорость сходимости ряда Фурье зависит от гладкости функции и поведения коэффициентов"
},
'function': {
'definition': "f(x) = { 2x + 3, -π ≤ x ≤ 0; 0, 0 < x ≤ π }",
'period': "2π",
'interval': "[-π, π]"
}
}
return description
class FourierSeriesMarkdownReport:
"""Класс для генерации полного отчета в Markdown"""
def __init__(self, analyzer: FourierSeriesAnalyzer, analysis_results: Dict[str, Any]):
self.analyzer = analyzer
self.results = analysis_results
def add_header(self, title: str, level: int = 1) -> str:
return f"{'#' * level} {title}\n\n"
def add_table(self, data: List[List[Any]], headers: List[str], title: str = "") -> str:
table_str = ""
if title:
table_str += f"**{title}**\n\n"
table_str += "| " + " | ".join(headers) + " |\n"
table_str += "|" + "|".join(["---"] * len(headers)) + "|\n"
for row in data:
table_str += "| " + " | ".join(map(str, row)) + " |\n"
table_str += "\n"
return table_str
def add_image(self, image_path: str, caption: str = "") -> str:
if os.path.exists(image_path):
# Центрированное изображение с ограниченной шириной
return (f'<div align="center">\n\n'
f'<img src="{image_path}" alt="{caption}" style="max-width: 80%; height: auto; border: 1px solid #ddd; padding: 5px; background: #f8f9fa;">\n\n'
f'**Рисунок:** {caption}\n\n'
f'</div>\n\n')
else:
return f"*Изображение не найдено: {caption}*\n\n"
def add_code_section(self) -> str:
success, src = read_own_source()
section = self.add_header("ПРИЛОЖЕНИЕ А", 2)
section += "**Исходный код программы**\n\n"
if success:
section += "```python\n" + src
if not src.endswith("\n"):
section += "\n"
section += "```\n"
else:
section += f"*Не удалось прочитать исходный код: {src}*\n"
return section
def generate_report(self) -> str:
report = ""
# Титульная страница
report += '<div style="page-break-after: always;">\n\n'
report += "# Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования\n\n"
report += "### «Казанский национальный исследовательский технологический университет»\n\n"
report += "#### Институт: Институт управления, автоматизации и информационных технологий\n"
report += "#### Кафедра Информатики и прикладной математики\n\n"
report += "---\n\n"
report += "# ЛАБОРАТОРНАЯ РАБОТА\n\n"
description = self.analyzer.get_analysis_description()
report += f"### по дисциплине: «{description['discipline']}»\n\n"
report += f"### на тему: «{description['topic']}»\n\n"
report += f"### {description['variant']}\n\n"
report += "---\n\n"
report += "**Выполнил:** \n"
report += "студент группы 851-М81 \n"
report += "Меркулов А. Д. \n"
report += '</div>\n\n'
# Содержание
report += self.add_header("СОДЕРЖАНИЕ", 1)
toc = [
"1. ВВЕДЕНИЕ",
"2. ПОСТАНОВКА ЗАДАЧИ",
"3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ",
" 3.1. Ряд Фурье для функций с периодом 2π",
" 3.2. Вычисление коэффициентов Фурье",
"4. АНАЛИТИЧЕСКОЕ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ",
" 4.1. Постоянная составляющая a₀",
" 4.2. Коэффициенты aₙ для косинусоидальных гармоник",
" 4.3. Коэффициенты bₙ для синусоидальных гармоник",
"5. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ",
" 5.1. Исходная функция",
" 5.2. Частичные суммы ряда Фурье",
" 5.3. Явление Гиббса",
" 5.4. Анализ сходимости",
"6. ВЫВОДЫ",
"ПРИЛОЖЕНИЕ А"
]
for item in toc:
report += f"{item}\n\n"
report += "---\n\n"
# 1) Введение
report += self.add_header("1. ВВЕДЕНИЕ", 1)
report += f"**Цель работы:** {description['purpose']}\n\n"
report += "**Задачи исследования:**\n"
for i, task in enumerate(description['tasks'], 1):
report += f"{i}. {task}\n"
report += "\n"
report += "**Актуальность исследования** обусловлена фундаментальной важностью рядов Фурье в математическом анализе, теории сигналов, физике и инженерных приложениях. Разложение функций в ряды Фурье позволяет анализировать сложные сигналы через их спектральные компоненты.\n\n"
# 2) Постановка задачи
report += self.add_header("2. ПОСТАНОВКА ЗАДАЧИ", 1)
func_def = description['function']
report += f"**Исследуемая функция:** {func_def['definition']}\n\n"
report += f"**Период:** {func_def['period']}\n\n"
report += f"**Интервал анализа:** {func_def['interval']}\n\n"
report += "**Задача:** Разложить заданную кусочно-линейную функцию в ряд Фурье на интервале [-π, π], проанализировать сходимость полученного ряда и исследовать явление Гиббса в окрестности точки разрыва.\n\n"
# 3) Теоретические основы
report += self.add_header("3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ", 1)
report += self.add_header("3.1. Ряд Фурье для функций с периодом 2π", 2)
methodology = description['methodology']
report += f"**{list(methodology.keys())[0]}:** {methodology['fourier_series']}\n\n"
report += "где:\n"
report += "- a₀/2 - постоянная составляющая\n"
report += "- aₙ - коэффициенты косинусоидальных гармоник\n"
report += "- bₙ - коэффициенты синусоидальных гармоник\n"
report += "- n - номер гармоники\n\n"
report += self.add_header("3.2. Вычисление коэффициентов Фурье", 2)
report += f"**{list(methodology.keys())[1]}:** {methodology['coefficients']}\n\n"
report += "**Интегралы вычисляются на интервале [-π, π]:**\n"
report += "- a₀ = (1/π) ∫₋πᵖ f(x) dx\n"
report += "- aₙ = (1/π) ∫₋πᵖ f(x) cos(nx) dx\n"
report += "- bₙ = (1/π) ∫₋πᵖ f(x) sin(nx) dx\n\n"
# 4) Аналитическое вычисление коэффициентов
report += self.add_header("4. АНАЛИТИЧЕСКОЕ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ", 1)
report += self.add_header("4.1. Постоянная составляющая a₀", 2)
report += "Вычисляем интеграл для a₀:\n"
report += "a₀ = (1/π) [∫₋π⁰ (2x + 3) dx + ∫₀ᵖ 0 dx]\n"
report += "a₀ = (1/π) [ [x² + 3x]₋π⁰ ]\n"
report += "a₀ = (1/π) [ (0) - (π² - 3π) ]\n"
report += "**a₀ = -π + 3**\n\n"
comparison = self.results['comparison']
report += f"**Численное значение:** a₀ = {comparison['a0_numerical']:.6f}\n"
report += f"**Аналитическое значение:** a₀ = {comparison['a0_analytical']:.6f}\n"
report += f"**Погрешность:** {comparison['a0_error']:.2e}\n\n"
report += self.add_header("4.2. Коэффициенты aₙ для косинусоидальных гармоник", 2)
report += "aₙ = (1/π) ∫₋π⁰ (2x + 3) cos(nx) dx\n"
report += "Интегрируя по частям, получаем:\n"
report += "**aₙ = (2/(πn²)) (1 - (-1)ⁿ)**\n\n"
report += "**Особенности:**\n"
report += "- При четных n: aₙ = 0\n"
report += "- При нечетных n: aₙ = 4/(πn²)\n\n"
# Таблица первых коэффициентов
an_comparison = self.results['comparison']['an_comparison']
an_data = []
for i, (num, anal) in enumerate(an_comparison, 1):
an_data.append([f"a_{i}", f"{num:.6f}", f"{anal:.6f}", f"{abs(num-anal):.2e}"])
report += self.add_table(an_data, ["Коэффициент", "Численное", "Аналитическое", "Погрешность"],
"Сравнение численных и аналитических значений aₙ")
report += self.add_header("4.3. Коэффициенты bₙ для синусоидальных гармоник", 2)
report += "bₙ = (1/π) ∫₋π⁰ (2x + 3) sin(nx) dx\n"
report += "Интегрируя по частям, получаем:\n"
report += "**bₙ = (1/(πn)) [-3 - (2π - 3)(-1)ⁿ]**\n\n"
# Таблица первых коэффициентов
bn_comparison = self.results['comparison']['bn_comparison']
bn_data = []
for i, (num, anal) in enumerate(bn_comparison, 1):
bn_data.append([f"b_{i}", f"{num:.6f}", f"{anal:.6f}", f"{abs(num-anal):.2e}"])
report += self.add_table(bn_data, ["Коэффициент", "Численное", "Аналитическое", "Погрешность"],
"Сравнение численных и аналитических значений bₙ")
# 5) Результаты исследования
report += self.add_header("5. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ", 1)
visualizations = self.results['visualizations']
report += self.add_header("5.1. Исходная функция", 2)
if 'original_function' in visualizations:
report += self.add_image(visualizations['original_function'],
"График исходной кусочно-заданной функции")
report += "**Анализ:** Функция имеет линейный участок на интервале [-π, 0] и постоянное нулевое значение на (0, π]. В точке x=0 наблюдается разрыв первого рода.\n\n"
report += self.add_header("5.2. Частичные суммы ряда Фурье", 2)
if 'fourier_comparison' in visualizations:
report += self.add_image(visualizations['fourier_comparison'],
"Сравнение исходной функции и частичных сумм ряда Фурье")
report += "**Анализ:** С увеличением количества гармоник частичные суммы ряда Фурье все лучше аппроксимируют исходную функцию. Наибольшие отклонения наблюдаются в окрестности точки разрыва.\n\n"
report += self.add_header("5.3. Явление Гиббса", 2)
if 'gibbs_phenomenon' in visualizations:
report += self.add_image(visualizations['gibbs_phenomenon'],
"Явление Гиббса в окрестности точки разрыва")
report += f"**{list(description['methodology'].keys())[2]}:** {description['methodology']['gibbs']}\n\n"
gibbs_analysis = self.results['gibbs_analysis']
report += "**Перерегулирование (overshoot) для различного количества гармоник:**\n"
for n, overshoot in gibbs_analysis['overshoots'].items():
report += f"- n={n}: {overshoot:.4f}\n"
report += "\n"
report += "**Наблюдения:** Явление Гиббса проявляется в виде выбросов частичных сумм ряда Фурье в окрестности точки разрыва. Амплитуда выбросов не стремится к нулю с увеличением количества гармоник, а стабилизируется около 9% от величины скачка.\n\n"
report += self.add_header("5.4. Анализ сходимости", 2)
if 'coefficients_decay' in visualizations:
report += self.add_image(visualizations['coefficients_decay'],
"Скорость убывания коэффициентов Фурье")
if 'approximation_error' in visualizations:
report += self.add_image(visualizations['approximation_error'],
"Зависимость погрешности аппроксимации от количества гармоник")
convergence = self.results['convergence_analysis']
report += f"**Скорость убывания коэффициентов:**\n"
report += f"- Коэффициенты aₙ: O(n^{convergence['slope_an']:.3f})\n"
report += f"- Коэффициенты bₙ: O(n^{convergence['slope_bn']:.3f})\n\n"
report += f"**{list(description['methodology'].keys())[3]}:** {description['methodology']['convergence']}\n\n"
# 6) Выводы
report += self.add_header("6. ВЫВОДЫ", 1)
conclusions = [
"Успешно выполнено разложение кусочно-заданной функции в ряд Фурье на интервале [-π, π]",
"Получены аналитические выражения для коэффициентов Фурье, подтвержденные численными расчетами",
"Установлено, что коэффициенты aₙ убывают как O(1/n²) для нечетных n и равны нулю для четных n",
"Коэффициенты bₙ убывают как O(1/n), что определяет общую скорость сходимости ряда",
"Обнаружено и проанализировано явление Гиббса в окрестности точки разрыва x=0",
"Показано, что с увеличением количества гармоник погрешность аппроксимации монотонно уменьшается",
"Ряд Фурье равномерно сходится к исходной функции во всех точках непрерывности",
"В точке разрыва ряд Фурье сходится к среднему арифметическому пределов функции слева и справа"
]
for i, conclusion in enumerate(conclusions, 1):
report += f"{i}. {conclusion}\n"
report += "\n"
# Приложение
report += self.add_code_section()
return report
class FourierSeriesDocxReport:
"""Класс для генерации отчета в формате DOCX"""
def __init__(self, analyzer: FourierSeriesAnalyzer, analysis_results: Dict[str, Any]):
self.analyzer = analyzer
self.results = analysis_results
def setup_document_styles(self, doc):
"""Настройка стилей документа"""
# Настройка стилей для русского текста
try:
doc.styles['Normal'].font.name = 'Times New Roman'
doc.styles['Normal']._element.rPr.rFonts.set(qn('w:eastAsia'), 'Times New Roman')
doc.styles['Normal'].font.size = Pt(12)
except:
pass
def add_table_to_docx(self, doc, data: List[List[Any]], headers: List[str], title: str = ""):
"""Добавляет таблицу в DOCX документ"""
if title:
p = doc.add_paragraph()
p.add_run(title).bold = True
p.alignment = WD_ALIGN_PARAGRAPH.CENTER
doc.add_paragraph()
table = doc.add_table(rows=len(data)+1, cols=len(headers))
table.style = 'Table Grid'
# Заголовки
hdr_cells = table.rows[0].cells
for i, header in enumerate(headers):
hdr_cells[i].text = str(header)
hdr_cells[i].paragraphs[0].alignment = WD_ALIGN_PARAGRAPH.CENTER
for paragraph in hdr_cells[i].paragraphs:
for run in paragraph.runs:
run.bold = True
# Данные
for i, row in enumerate(data, 1):
row_cells = table.rows[i].cells
for j, cell in enumerate(row):
row_cells[j].text = str(cell)
if j > 0: # Выравнивание числовых данных по центру
row_cells[j].paragraphs[0].alignment = WD_ALIGN_PARAGRAPH.CENTER
doc.add_paragraph()
def add_image_to_docx(self, doc, image_path: str, caption: str = ""):
"""Добавляет изображение в DOCX документ"""
if os.path.exists(image_path):
try:
# Центрируем изображение
paragraph = doc.add_paragraph()
paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
run = paragraph.add_run()
run.add_picture(image_path, width=Inches(5.0))
# Добавляем подпись
if caption:
caption_paragraph = doc.add_paragraph()
caption_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
caption_run = caption_paragraph.add_run(f"Рисунок: {caption}")
caption_run.italic = True
doc.add_paragraph()
except Exception as e:
doc.add_paragraph(f"Ошибка при добавлении изображения: {e}")
else:
doc.add_paragraph(f"Изображение не найдено: {caption}")
def generate_docx_report(self, filename: str = "fourier_series_report.docx") -> str:
"""
Генерация отчёта в формате DOCX для анализа рядов Фурье
"""
out_path = os.path.join("results", filename)
if not PYDOCX_AVAILABLE:
print("python-docx не установлен — DOCX отчёт не будет создан")
return out_path
try:
doc = Document()
self.setup_document_styles(doc)
# Титульная страница
title_paragraph = doc.add_paragraph()
title_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
title_run = title_paragraph.add_run("Федеральное государственное бюджетное образовательное учреждение\высшего профессионального образования\n«Казанский национальный исследовательский технологический университет»")
title_run.bold = True
title_run.font.size = Pt(14)
doc.add_paragraph()
university_paragraph = doc.add_paragraph()
university_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
university_paragraph.add_run("Институт: Институт управления, автоматизации и информационных технологий\nКафедра Информатики и прикладной математики").bold = True
doc.add_paragraph("\n" * 3)
# Название работы
work_paragraph = doc.add_paragraph()
work_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
work_run = work_paragraph.add_run("ЛАБОРАТОРНАЯ РАБОТА")
work_run.bold = True
work_run.font.size = Pt(16)
description = self.analyzer.get_analysis_description()
doc.add_paragraph()
discipline_paragraph = doc.add_paragraph()
discipline_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
discipline_paragraph.add_run(f"по дисциплине: «{description['discipline']}»").bold = True
doc.add_paragraph()
topic_paragraph = doc.add_paragraph()
topic_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
topic_paragraph.add_run(f"на тему: «{description['topic']}»").bold = True
doc.add_paragraph()
variant_paragraph = doc.add_paragraph()
variant_paragraph.alignment = WD_ALIGN_PARAGRAPH.CENTER
variant_paragraph.add_run(f"{description['variant']}").bold = True
doc.add_paragraph("\n" * 4)
# Информация о студенте и преподавателе
info_table = doc.add_table(rows=4, cols=2)
info_table.style = 'Table Grid'
info_table.cell(0, 0).text = "Выполнил:"
info_table.cell(0, 1).text = "студент группы 851-М81\nМеркулов А. Д."
for row in info_table.rows:
for cell in row.cells:
cell.paragraphs[0].alignment = WD_ALIGN_PARAGRAPH.LEFT
doc.add_page_break()
# Содержание
title = doc.add_paragraph()
title.alignment = WD_ALIGN_PARAGRAPH.CENTER
title.add_run("СОДЕРЖАНИЕ").bold = True
title.runs[0].font.size = Pt(14)
doc.add_paragraph()
toc_items = [
"1. ВВЕДЕНИЕ",
"2. ПОСТАНОВКА ЗАДАЧИ",
"3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ",
"3.1. Ряд Фурье для функций с периодом 2π",
"3.2. Вычисление коэффициентов Фурье",
"4. АНАЛИТИЧЕСКОЕ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ",
"4.1. Постоянная составляющая a₀",
"4.2. Коэффициенты aₙ",
"4.3. Коэффициенты bₙ",
"5. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ",
"5.1. Исходная функция",
"5.2. Частичные суммы ряда Фурье",
"5.3. Явление Гиббса",
"6. ВЫВОДЫ",
"ПРИЛОЖЕНИЕ А"
]
for item in toc_items:
p = doc.add_paragraph()
p.add_run(item)
doc.add_page_break()
# 1) Введение
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("1. ВВЕДЕНИЕ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
doc.add_paragraph(f"Цель работы: {description['purpose']}")
doc.add_paragraph("Задачи исследования:")
for task in description['tasks']:
p = doc.add_paragraph(task, style='List Bullet')
# 2) Постановка задачи
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("2. ПОСТАНОВКА ЗАДАЧИ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
func_def = description['function']
doc.add_paragraph(f"Исследуемая функция: {func_def['definition']}")
doc.add_paragraph(f"Период: {func_def['period']}")
doc.add_paragraph(f"Интервал анализа: {func_def['interval']}")
# 3) Теоретические основы
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("3. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
subheading = doc.add_paragraph()
subheading.add_run("3.1. Ряд Фурье для функций с периодом 2π").bold = True
methodology = description['methodology']
doc.add_paragraph(f"Ряд Фурье: {methodology['fourier_series']}")
subheading = doc.add_paragraph()
subheading.add_run("3.2. Вычисление коэффициентов Фурье").bold = True
doc.add_paragraph(f"Коэффициенты Фурье: {methodology['coefficients']}")
# 4) Аналитическое вычисление коэффициентов
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("4. АНАЛИТИЧЕСКОЕ ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
subheading = doc.add_paragraph()
subheading.add_run("4.1. Постоянная составляющая a₀").bold = True
comparison = self.results['comparison']
doc.add_paragraph(f"Аналитическое значение: a₀ = -π + 3 ≈ {comparison['a0_analytical']:.6f}")
doc.add_paragraph(f"Численное значение: a₀ = {comparison['a0_numerical']:.6f}")
subheading = doc.add_paragraph()
subheading.add_run("4.2. Коэффициенты aₙ").bold = True
# Таблица коэффициентов aₙ
an_comparison = self.results['comparison']['an_comparison'][:5]
an_data = []
for i, (num, anal) in enumerate(an_comparison, 1):
an_data.append([f"a_{i}", f"{num:.6f}", f"{anal:.6f}"])
self.add_table_to_docx(doc, an_data, ["Коэффициент", "Численное", "Аналитическое"],
"Коэффициенты aₙ")
subheading = doc.add_paragraph()
subheading.add_run("4.3. Коэффициенты bₙ").bold = True
# Таблица коэффициентов bₙ
bn_comparison = self.results['comparison']['bn_comparison'][:5]
bn_data = []
for i, (num, anal) in enumerate(bn_comparison, 1):
bn_data.append([f"b_{i}", f"{num:.6f}", f"{anal:.6f}"])
self.add_table_to_docx(doc, bn_data, ["Коэффициент", "Численное", "Аналитическое"],
"Коэффициенты bₙ")
# 5) Результаты исследования
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("5. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
visualizations = self.results['visualizations']
subheading = doc.add_paragraph()
subheading.add_run("5.1. Исходная функция").bold = True
if 'original_function' in visualizations:
self.add_image_to_docx(doc, visualizations['original_function'],
"Исходная кусочно-заданная функция")
subheading = doc.add_paragraph()
subheading.add_run("5.2. Частичные суммы ряда Фурье").bold = True
if 'fourier_comparison' in visualizations:
self.add_image_to_docx(doc, visualizations['fourier_comparison'],
"Сравнение исходной функции и частичных сумм ряда Фурье")
subheading = doc.add_paragraph()
subheading.add_run("5.3. Явление Гиббса").bold = True
if 'gibbs_phenomenon' in visualizations:
self.add_image_to_docx(doc, visualizations['gibbs_phenomenon'],
"Явление Гиббса в окрестности точки разрыва")
# 6) Выводы
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("6. ВЫВОДЫ").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
conclusions = [
"Успешно выполнено разложение кусочно-заданной функции в ряд Фурье",
"Получены аналитические выражения для коэффициентов Фурье",
"Установлена скорость убывания коэффициентов Фурье",
"Обнаружено и проанализировано явление Гиббса",
"Показана сходимость ряда Фурье к исходной функции",
"Подтверждена эффективность численных методов вычисления коэффициентов"
]
for i, conclusion in enumerate(conclusions, 1):
doc.add_paragraph(f"{i}. {conclusion}", style='List Number')
# Приложение
doc.add_page_break()
heading = doc.add_paragraph()
heading.alignment = WD_ALIGN_PARAGRAPH.CENTER
heading.add_run("ПРИЛОЖЕНИЕ А").bold = True
heading.runs[0].font.size = Pt(14)
doc.add_paragraph()
subheading = doc.add_paragraph()
subheading.add_run("Исходный код программы").bold = True
success_src, src_text = read_own_source()
if success_src:
# Добавляем код с моноширинным шрифтом
for line in src_text.splitlines():
p = doc.add_paragraph()
run = p.add_run(line)
try:
run.font.name = 'Courier New'
run.font.size = Pt(9)
except Exception:
pass
else:
doc.add_paragraph("Не удалось прочитать исходный код скрипта: " + src_text)
# Сохранение файла
doc.save(out_path)
print(f"DOCX-отчёт сохранён: {out_path}")
except Exception as e:
print(f"Ошибка при генерации DOCX-отчёта: {e}")
raise e
return out_path
def main():
"""Основная функция для выполнения лабораторной работы по рядам Фурье"""
# Создаем анализатор
analyzer = FourierSeriesAnalyzer()
# Выполняем анализ
print("Выполняется анализ разложения функции в ряд Фурье...")
results = analyzer.analyze()
# Создаем папку для результатов
os.makedirs("results", exist_ok=True)
os.makedirs("results/images", exist_ok=True)
# Генерируем Markdown отчет
md_reporter = FourierSeriesMarkdownReport(analyzer, results)
md_report = md_reporter.generate_report()
# Сохраняем Markdown отчет
with open("README.md", "w", encoding="utf-8") as f:
f.write(md_report)
print("Markdown отчет сохранен: README.md")
# Генерируем DOCX отчет
docx_reporter = FourierSeriesDocxReport(analyzer, results)
docx_path = docx_reporter.generate_docx_report()
# Выводим основные результаты в консоль
print("\n" + "="*80)
print("РЕЗУЛЬТАТЫ АНАЛИЗА РАЗЛОЖЕНИЯ В РЯД ФУРЬЕ")
print("="*80)
comparison = results['comparison']
print(f"\nКОЭФФИЦИЕНТЫ ФУРЬЕ:")
print("-" * 50)
print(f"a₀ (численный): {comparison['a0_numerical']:.6f}")
print(f"a₀ (аналитический): {comparison['a0_analytical']:.6f}")
print(f"Погрешность a₀: {comparison['a0_error']:.2e}")
print(f"\nПЕРВЫЕ КОЭФФИЦИЕНТЫ aₙ:")
print("-" * 50)
for i, (num, anal) in enumerate(results['comparison']['an_comparison'][:5], 1):
error = abs(num - anal)
print(f"a_{i}: числ={num:.6f}, анал={anal:.6f}, погр={error:.2e}")
convergence = results['convergence_analysis']
print(f"\nАНАЛИЗ СХОДИМОСТИ:")
print("-" * 50)
print(f"Скорость убывания aₙ: O(n^{convergence['slope_an']:.3f})")
print(f"Скорость убывания bₙ: O(n^{convergence['slope_bn']:.3f})")
gibbs = results['gibbs_analysis']
print(f"\nЯВЛЕНИЕ ГИББСА:")
print("-" * 50)
for n, overshoot in gibbs['overshoots'].items():
print(f"n={n}: перерегулирование = {overshoot:.4f}")
print(f"\nВИЗУАЛИЗАЦИИ СОЗДАНЫ:")
print("-" * 50)
for name, path in results['visualizations'].items():
if os.path.exists(path):
print(f"✓ {name}: {path}")
print(f"\nОТЧЕТЫ СОХРАНЕНЫ:")
print("-" * 50)
print(f"✓ Markdown отчет: README.md")
if PYDOCX_AVAILABLE:
print(f"✓ DOCX отчет: {docx_path}")
return results
if __name__ == "__main__":
main()